Таблицы удельной теплоемкости веществ (газов, жидкостей и др.)

Равновесные процессы. Максимальная работа

Ранее отмечалось,
что при расширении газ производит работу
только в том случае, если при этом он
преодолевает сопротивление. Пусть
имеется цилиндр с поршнем, который
наполнен идеальным газом при некотором
давлении р₁.
Объем цилиндра V₁.
Пусть при расширении поршень сместился
из исходного положения 1 в положение 2.
При этом объем газа увеличился на
величину V.
Естественно произошло уменьшение
давления. Но если
V₁
>> V,
то происходящими изменениями можно
пренебречь и считать
р₁
= const.
Но производимая работа при расширении
газа от величины р₁
вообще не зависит, она определяется
лишь величиной V
и преодолеваемым поршнем давлением,
которое обозначим как р₂.
Если р₁
>> р₂,
то движение поршня слева направо возможно
и, следовательно, газ в этом случае может
производить работу А = Vр₂.

Причем, чем больше
р₂,
тем больше и производимая им работа. Но
возрастание р₂
не беспредельно. Дело в том, что при р₂1
поршень будет двигаться в обратном
направлении и работа будет производиться
не системой, то есть газом в объеме V₁,
а над системой. Иначе говоря, она изменит
свой знак. Следовательно, максимальная
работа, производимая газом наблюдается
при р₁
= р₂
равна р₂V.
Причем сама система в этом случае
находится в равновесии. Следовательно,
в реальных условиях р₁
всегда больше р₂
и никогда нельзя получить максимальную
работу, равную

,

где n
– число моль газа, а R
– универсальная газовая постоянная.
Так как в случае идеального газа,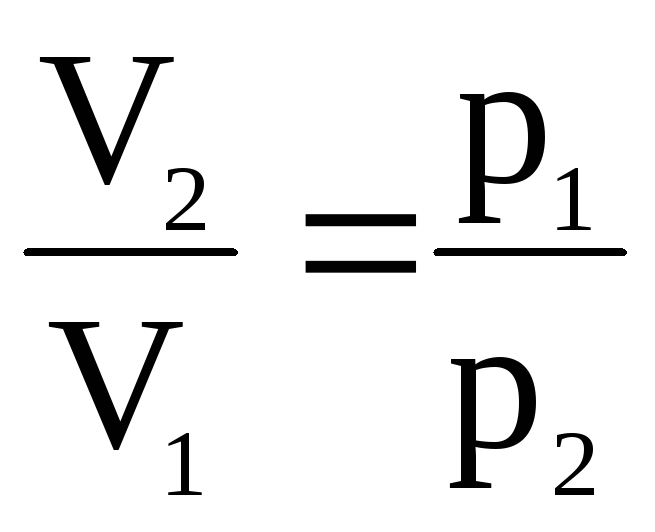
то

.

Аmax
никогда реально получить нельзя, но
знать ее очень важно, так как она является
мерилом качества использованных
возможностей тепловой машины. Вместе
с тем, все реальные процессы, протекающие
с конечной скоростью необратимы, так
как их движущая сила всегда больше
преодолеваемой. (Скорость протекания
равновесных процессов бесконечно мала,
а сами они протекают бесконечно большое
время)

Воображаемый процесс, протекающий
при р1
= р2,
представляет собой непрерывный ряд
равновесий. Такие процессы, называемые
равновесными, протекающими с одинаковой
вероятностью слева направо и наоборот

(Скорость протекания
равновесных процессов бесконечно мала,
а сами они протекают бесконечно большое
время). Воображаемый процесс, протекающий
при р1
= р2,
представляет собой непрерывный ряд
равновесий. Такие процессы, называемые
равновесными, протекающими с одинаковой
вероятностью слева направо и наоборот.

Высокая удельная теплоемкость

При обработке металлов применяют водные растворы минеральных солей ( электролитов), органических ПАВ, а также смесей этих веществ. Водные растворы имеют следующие достоинства: высокую удельную теплоемкость и теплопроводность, благодаря которым обеспечивается эффективное охлаждение инструмента в зоне резания; прозрачность, дающую возможность наблюдать за зоной обработки металла в процессе работы; стабильность при хранении ( коллоидная, химическая, бактериологическая); простота приготовления и невысокая стоимость.
 

Вода является наиболее широко применяемым средством тушения пожаров, связанных с горением различных веществ и материалов. Достоинствами воды являются ее дешевизна и доступность, относительно высокая удельная теплоемкость, высокая скрытая теплота испарения, химическая инертность по отношению к большинству веществ и материалов.
 

Связанные частоты и связанные постоянные для расчета удельной теплоемкости газов, паров и жидкостей.

Реальная удельная теплоемкость одноатомных газов при температурах, существенно больших температуры насыщения, действительно имеет значения, предсказываемые кинетической теорией газов. Двухатомные и многоатомные газы имеют, однако, более высокие удельные теплоемкости вследствие упругих колебаний молекул, которыми пренебрегает эта теория. С ростом температуры число столкновений, удовлетворяющих этому требованию, также растет, таким образом увеличивая вклад колебательной энергии в полную энергию многоатомного ( но по-прежнему идеального) газа.
 

Основным огнетушащим эффектом воды — наиболее распространенного и высокоэффективного огнетушащего вещества — является охлаждение. Оно достигается благодаря хорошему теплопоглощению, причиной которого являются высокая удельная теплоемкость и высокая теплота парообразования.
 

Изменение температуры застывания углеводородов различных классов.

При 20 удельные теплоемкости углеводородов всех классов составляют примерноО 4 — 0 5 ккал / кг-град. Как видно из рис. 38, при данной температуре кипения наиболее высокой удельной теплоемкостью обладают алканы; удельная теплоемкость алкеновых углеводородов несколько ниже; наименьшую теплоемкость имеют тяжелые ароматические углеводороды.
 

Вода — — наиболее распространенная охлаждающая жидкость. Она доступна, безопасна в пожарном отношении, безвредна для человека и имеет высокую удельную теплоемкость — 4 19 кДж / ( ног К), превосходящую все другие известные охлаждающие жидкости. Существенным недостатком является высокая температура замерзания ( вода замерзает при температуре 0 С со значительным ( увеличением объема), что вызывает разрушение ( размораживание) системы охлаждения при низких температурах.
 

Несмотря на низкую температуру плавления, алюминий требует для расплавления большого количества тепла благодаря своей высокой удельной теплоемкости. Механические свойства чистого алюминия невысоки.
 

Наиболее подходящими материалами для защиты ракет и других летательных аппаратов от абляции ( эрозии) при вхождении их в плотные слои атмосферы являются пластмассы. Часть пластмассы при этом выгорает, она подвергается эндотермическому разложению с выделением газов, имеющих высокую удельную теплоемкость ( СН4, С2Н2, С2Н4, Н2 и др.) — Кроме того, образуется поверхностный теплозащитный слой в виде кокса. В процессе абляции поверхностного слоя наполнители пластмасс оплавляются и частично разлагаются.
 

В том и другом виде хладоагент должен, в первую очередь, быть химически инертным к той среде, с которой вводится в соприкосновение, термически стойким в пределах рабочих температур, должен хорошо отделяться от уловленных продуктов окисления, недорогим и легкодоступным. Кроме того, жидкий хладоагент должен быть нетоксичным, иметь возможно более низкую упругость паров и высокую удельную теплоемкость, не действовать коррозионно на аппаратуру.
 

Несмотря на низкую температуру плавления ( — 660) алюминий требует для расплавления большого количества тепла, что объясняется его высокой удельной теплоемкостью и чрезвычайно высокой скрытой теплотой плавления ( 93 кал.
 

График температур при предварительном.

Последнее следует из хорошей сходимости расчетного ряда. Вообще говоря, подобный подход к расчету нестационарного поля с источниками тепла может привести к значительным погрешностям, особенно при расчете температурного поля тел незначительной теплопроводности и высокой удельной теплоемкости с источниками тепла, сосредоточенными в малых относительно объема тела областях.
 

Максимальная и минимальная теплоты процесса

Уравнения первого закона термодинамики
в сложных закрытых ТС при двух фиксированных
параметрах имеют вид:

— для изохорно-изотермического процесса
(T,V=const):ℒ_Т,V;

— для изобарно-изотермического процесса
(T,p=const):
ℒ_Т,р.

При написании этих уравнений использовалось
правило знаков, принятое в термодинамике,
т.е.,
если теплота подводится к ТС, иℒ>0,
если работа совершается термодинамической
системой. В термохимии принято
противоположное правило знаков для
теплоты, т.е. теплота,
(положительна), если она отводится от
ТС. Тогда для конечных процессов 1-2
уравнение 1-го закона термодинамики
будет иметь вид:

ℒ_Т,V, (1)

ℒ_Т,р, (2)

Соотношения (1) и (2) справедливы для любых
процессов, обратимых и необратимых.

Для обратимого процесса
ℒ=ℒ_max ,:

ℒ_Т,Vmax, (3)

ℒ_Т,pmax, (4)

Для максимально возможного необратимого
процесса ℒ=ℒ_min=0,:

, (5)

.(6)

Соотношения (5) и (6) используются в
химической термодинамике для расчета
изохорного и изобарного тепловых
эффектов химических реакций (ТЭХР). В
этом случае работа ℒ_maxпреобразуется в тепловую энергию
неупорядоченного движения частиц (в
теплоту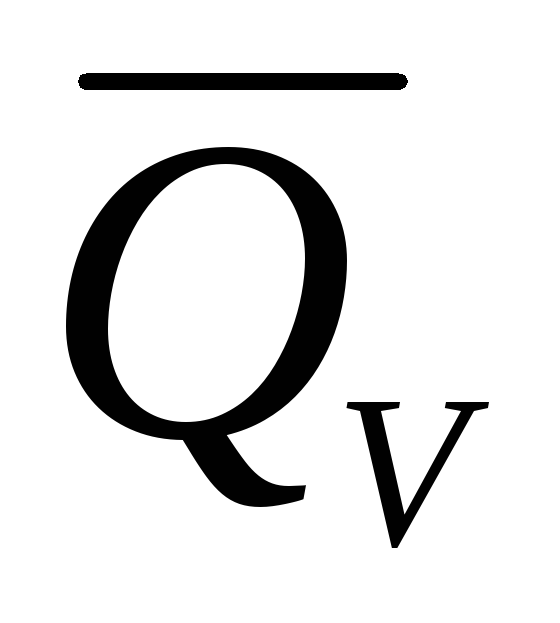и).

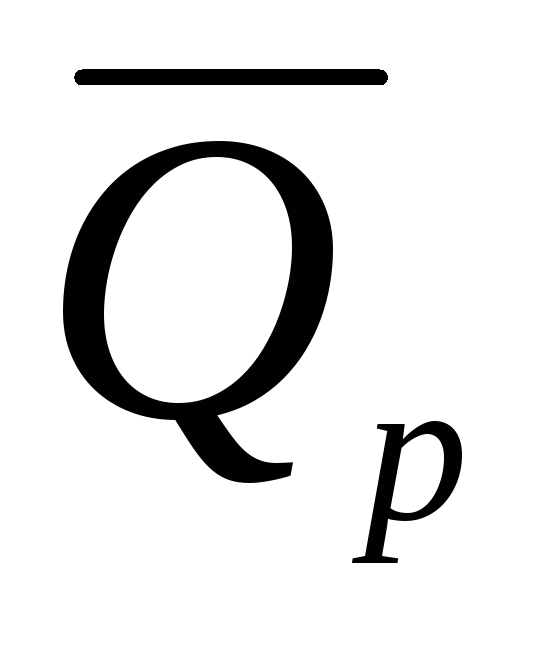В случае обратимого равновесного
процесса перераспределения масс
(уравнения (3) и (4)) величины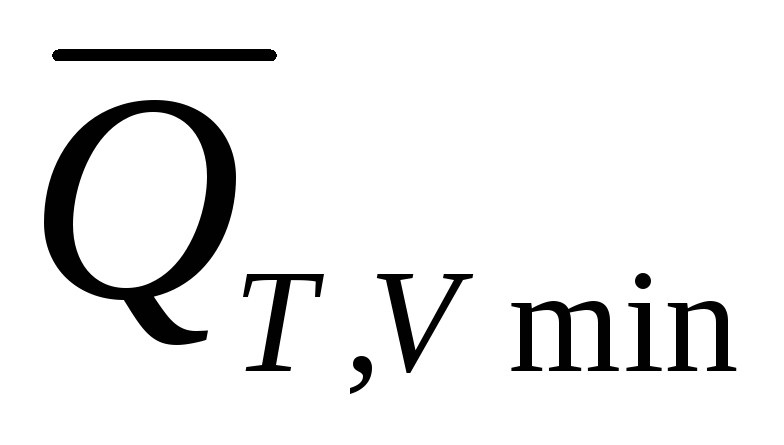и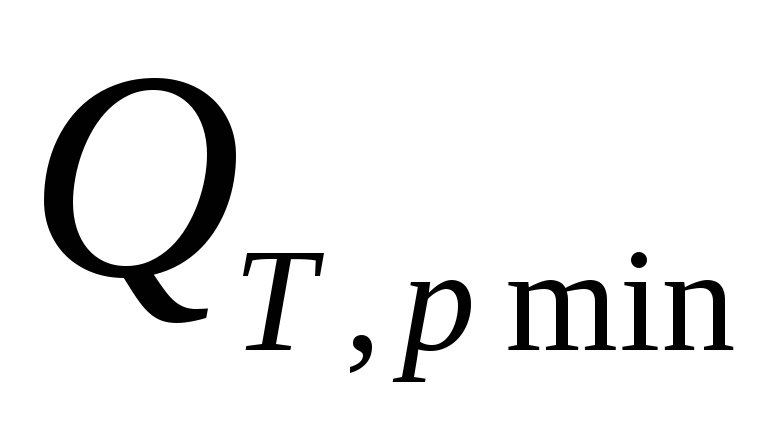— это количества теплоты, которыми ТС
обменивается с окружающей средой в
процессахи.ℒ_Т,Vmaxиℒ_Т,pmax— максимальные количества работы
немеханического характера, которые
могут быть получены от ТС в процессахи.

В случае необратимого процесса
перераспределения массы в соответствии
со вторым законом термодинамики работаℒ_maxпреобразуется в теплоту, количество
которого равно изменению внутренней
энергии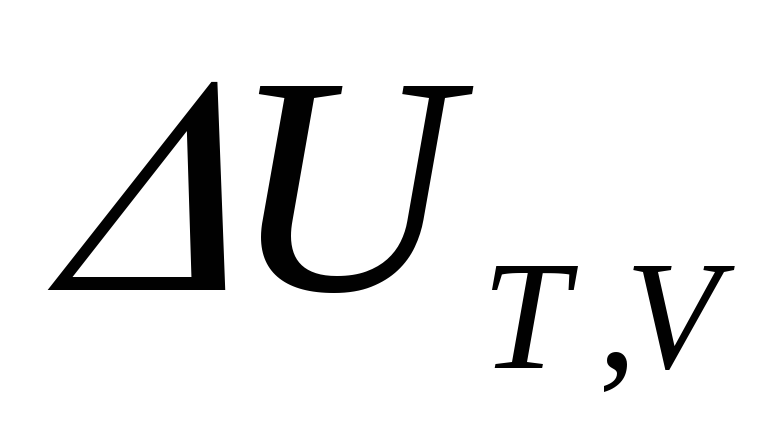в процессе,
или изменению энтальпии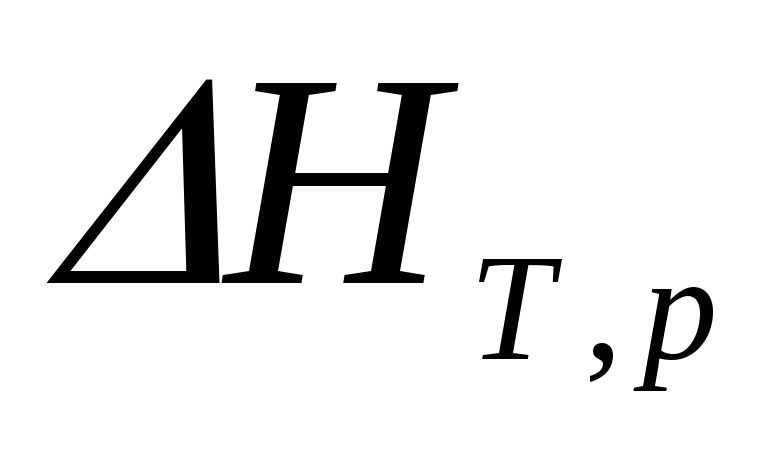в процессе,
протекающем в сложных термодинамических
системах.

Химические реакции, при которых теплота
отводится от термодинамической системы,
чтобы конечные продукты имели ту же
температуру, что и начальные реагенты,
называются экзотермическими химическими
реакциями. Химические реакции,
сопровождающиеся поглощением теплоты,
приT=const, называются эндотермическими химическими
реакциями.

Рассмотрим два примера: 1. разрядка
химического источника электроэнергии
(аккумулятор, батарея карманного фонаря)
– процесс обратимый: ℒ_Т,pmax— преобразуется в электрическую энергию,
а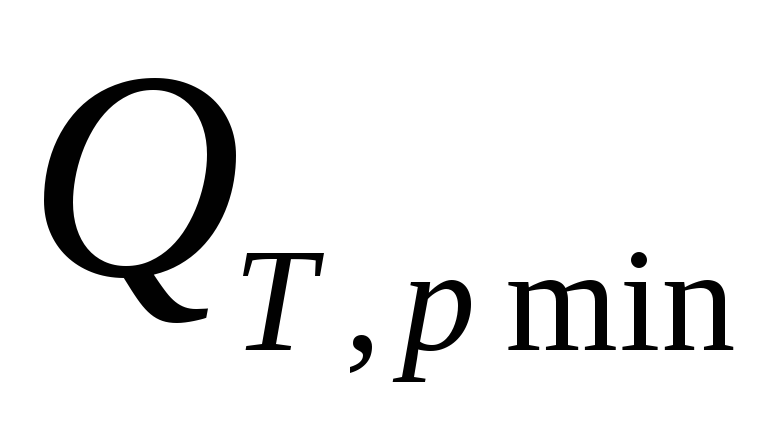— отводится от системы. 2. Если замкнуть
клеммы батареи накоротко, то получим
максимально необратимый процесс:ℒ,.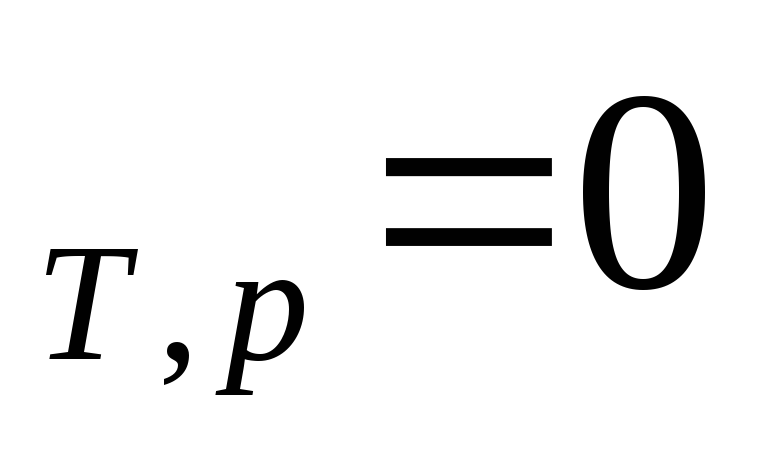

Таблица удельной теплоемкости пищевых продуктов

В таблице приведены значения средней удельной теплоемкости пищевых продуктов (овощей, фруктов, мяса, рыбы, хлеба, вина и т. д.) в диапазоне температуры 5…20°С и нормальном атмосферном давлении.

Таблица удельной теплоемкости продуктов питания

Продукты	C, Дж/(кг·К)
Абрикосы	3770
Ананасы	3684
Апельсины	3730
Арбуз	3940
Баклажаны	3935
Брюква	3810
Ветчина	2140
Вино крепленое	3690
Вино сухое	3750
Виноград	3550
Вишня	3650
Говядина и баранина жирная	2930
Говядина и баранина маложирная	3520
Горох	3684
Грибы свежие	3894
Груши	3680
Дрожжи прессованные	1550…3516
Дыни	3850
Ежевика	3642
Земляника	3684
Зерно пшеничное	1465…1549
Кабачки	3900
Капуста	3940
Картофель	3430
Клубника	3810
Колбасы	1930…2810
Крыжовник	3890
Лимоны	3726
Лук	2638
Макароны не приготовленные	1662
Малина	3480
Мандарины	3770
Маргарин сливочный	2140…3182
Масло анисовое	1846
Масло мятное	2080
Масло сливочное	2890…3100
Масло сливочное топленое	2180
Мед	2300…2428
Молоко сухое	1715…2090
Морковь	3140
Мороженое (при -10С)	2175
Мука	1720
Огурцы	4060
Пастила	2090
Патока	2512…2700
Перец сладкий	3935
Печенье	2170
Помидоры	3980
Пряники	1800…1930
Редис	3970
Рыба жирная	2930
Рыба нежирная	3520
Салат зеленый	4061
Сало топленое	2510
Сахар кусковой	1340
Сахарный песок	720
Свекла	3340
Свинина жирная	260
Свинина нежирная	3010
Слива	3750
Сметана	3010
Смородина черная	3740
Сода	2256
Соль поваренная (2% влажности)	920
Спаржа	3935
Сыр жирный	2430
Творог	3180
Телятина жирная	3180
Телятина нежирная	3520
Тесто заварное	2910
Тыква	3977
Хлеб (корка)	1680
Хлеб (мякиш)	2800
Черешня	3770
Чернослив	3181
Чеснок	3140
Шоколад	2340…2970
Шпинат	3977
Яблоки	3760
Яйцо куриное	3180

Кроме таблиц удельной теплоемкости, вы также можете ознакомиться с подробнейшей таблицей плотности веществ и материалов, которая содержит данные по величине плотности более 500 веществ (металлов, пластика, резины, продуктов, стекла и др.).

1. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов, изд. 3-е, перераб. и доп. — М.: «Энергия», 1975.
2. Тепловые свойства металлов и сплавов. Справочник. Лариков Л. Н., Юрченко Ю. Ф. — Киев: Наукова думка, 1985. — 439 с.
3. Физические величины. Справочник. А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др. Под ред. И. С. Григорьева — М.: Энергоатомиздат, 1991. — 1232 с.
4. Еремкин А. И., Королева Т. И. Тепловой режим зданий: Учебное пособие. — М.: Издательство ACB, 2000 — 368 с.
5. Кириллов П. Л., Богословская Г. П. Тепломассобмен в ядерных энергетических установках: Учебник для вузов.
6. Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е, стереотип. М.: «Энергия», 1977. — 344 с. с ил.
7. Казанцев Е. И. Промышленные печи. Справочное руководство для расчетов и проектирования.
8. Франчук А. У. Таблицы теплотехнических показателей строительных материалов, М.: НИИ строительной физики, 1969 — 142 с.
9. Добрынин В. М., Вендельштейн Б. Ю., Кожевников Д. А. Петрофизика: Учеб. для вузов. 2-ое изд. перераб. и доп. под редакцией доктора физико-математических наук Д. А. Кожевникова — М.: ФГУП Издательство «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2004. — 368 с., ил.
10. В. Блази. Справочник проектировщика. Строительная физика. М.: Техносфера, 2005. — 536 с.
11. Енохович А. С. Справочник по физике. М.: «Просвещение», 1978. — 415 с. с ил.
12. Строительная теплотехника СНиП II-3-79. Минстрой России — Москва 1995.
13. Мустафаев Р. А. Теплофизические свойства углеводородов при высоких параметрах состояния. М.: Энергоатомиздат, 1991. — 312 с.
14. Новиченок Н. Л., Шульман З. П. Теплофизические свойства полимеров. Минск, «Наука и техника» 1971. — 120 с.
15. Шелудяк Ю. Е., Кашпоров Л. Я. и др. Теплофизические свойства компонентов горючих систем. М., 1992. — 184 с.

Виды теплопередачи

Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.

Теплопроводность

Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.

Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.

Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.

Конвекция

Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.

Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.

Излучение

Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.

Если мы греемся у камина, то получаем тепло конвекцией или излучением?

Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.

Физическая основа теплоемкости

Температура образца вещества отражает среднее значение кинетическая энергия составляющих его частиц (атомов или молекул) относительно его центра масс. Однако не вся энергия, передаваемая образцу вещества, идет на повышение его температуры, примером чего является теорема о равнораспределении.

Одноатомные газы

Квантовая механика предсказывает, что при комнатной температуре и обычном давлении изолированный атом в газе не может хранить какое-либо значительное количество энергии, кроме как в форме кинетической энергии. Таким образом, теплоемкость на моль одинаково для всех одноатомных газов (например, благородных газов). Точнее, cV,м=3р2≈{ Displaystyle c_ {V, mathrm {m}} = 3R / 2 приблизительно {}}12,5 Дж / К / моль и cп,м=5р2≈{ Displaystyle c_ {P, mathrm {m}} = 5R / 2 приблизительно {}}21 Дж / К / моль, где р≈{ Displaystyle R приблизительно {}}8,31446 Дж / К / моль — это установка идеального газа (который является продуктом Постоянная преобразования Больцмана из кельвин микроскопическая единица энергии к макроскопической единице энергии джоуль, и Число Авогадро).

Следовательно, удельная теплоемкость (на единицу массы, а не на моль) одноатомного газа будет обратно пропорциональна его (размерной) атомный вес А{ displaystyle A}. То есть примерно

cV≈{ displaystyle c_ {V} приблизительно {}}12470 Дж / К / кгАcп≈{ displaystyle / A quad quad quad c_ {p} приблизительно {}}20785 Дж / К / кгА{ displaystyle / A}

Для благородных газов, от гелия до ксенона, эти расчетные значения равны

Газ	Он	Ne	Ar	Kr	Xe
А{ displaystyle A}	4.00	20.17	39.95	83.80	131.29
cV{ displaystyle c_ {V}} (Дж / К / м3)	3118	618.3	312.2	148.8	94.99
cп{ displaystyle c_ {p}} (Дж / К / кг)	5197	1031	520.3	248.0	158.3

Многоатомные газы

С другой стороны, многоатомная молекула газа (состоящая из двух или более связанных вместе атомов) может накапливать тепловую энергию в других формах, помимо своей кинетической энергии. Эти формы включают вращение молекулы и колебание атомов относительно ее центра масс.

Эти дополнительные степени свободы или «режимы» вносят вклад в удельную теплоемкость вещества. А именно, когда в газ с многоатомными молекулами вводится тепловая энергия, только часть ее идет на увеличение их кинетической энергии и, следовательно, температуры; остальное перейдет в те другие степени свободы. Чтобы достичь такого же повышения температуры, моль этого вещества должен быть передан большей тепловой энергии, чем моль одноатомного газа. Следовательно, теплоемкость многоатомного газа зависит не только от его молекулярной массы, но и от числа степеней свободы, которые имеют молекулы.

Квантовая механика далее утверждает, что каждая вращательная или колебательная мода может забирать или терять энергию только в определенном дискретном количестве (квантах). В зависимости от температуры, средняя тепловая энергия на молекулу может быть слишком маленькой по сравнению с квантами, необходимыми для активации некоторых из этих степеней свободы. Эти режимы называются «замороженными». В этом случае удельная теплоемкость вещества будет увеличиваться с температурой, иногда ступенчато, по мере того, как больше режимов размораживаются и начинают поглощать часть подводимой тепловой энергии.

Например, молярная теплоемкость азот N₂ при постоянной громкости cV,м={ displaystyle c_ {V, mathrm {m}} = {}} 20,6 Дж / К / моль (при 15 ° C, 1 атм), что составляет 2,49р{ displaystyle R}. Это значение, ожидаемое из теории, если каждая молекула имеет 5 степеней свободы. Оказывается, это три градуса вектора скорости молекулы плюс два градуса ее вращения вокруг оси, проходящей через центр масс и перпендикулярной линии двух атомов. Из-за этих двух дополнительных степеней свободы удельная теплоемкость cV{ displaystyle c_ {V}} из N₂ (736 Дж / К / кг) в 5/3 раза больше, чем у гипотетического одноатомного газа с той же молекулярной массой 28 (445 Дж / К / кг).

Это значение удельной теплоемкости азота практически постоянно от -150 ° C до примерно 300 ° C. В этом температурном диапазоне две дополнительные степени свободы, соответствующие колебаниям атомов, растяжению и сжатию связи, все еще «заморожены». Примерно при этой температуре эти режимы начинают «размораживаться», и в результате cV{ displaystyle c_ {V}} сначала начинает быстро увеличиваться, затем медленнее по мере приближения к другому постоянному значению. Оно составляет 35,5 Дж / К / моль при 1500 ° C, 36,9 при 2500 ° C и 37,5 при 3500 ° C. Последнее значение почти точно соответствует предсказанному значению для 7 степеней свободы на молекулу.

Изохорная теплоемкость

Изменение энтропии ds.

Вычислим изохорную теплоемкость влажного водяного пара, имеющего степень сухости х 0 575 при давлении 1 бар. Поданным опытов А. М. Керимова, теплоемкости су и су при давлении р 1 бар равны соответственно 1 007 и 16 95 ккал / кг. Непосредственное вычисление по таблицам водяного пара дает значение cv 10 1 ккал / ( кг — град), практически не отличающееся от экспериментального.

Так как изохорная теплоемкость влажного пара cv — величина положительная, то это значит, что знаки дифференциалов dp и dv противоположны.

Так как изохорная теплоемкость влажного пара cv — величина положительная, то величины dp и dv — противоположны. Таким образом, изоэнтропическое расширение влажного пара обусловливает уменьшение его давления и температуры, а изоэнтропическое сжатие — возрастание их.

Так как изохорная теплоемкость влажного пара с есть положительная величина, то отсюда следует, что знаки дифференциалов dp и dv противоположны.

Результаты исследований изохорной теплоемкости на изохорах, проведенные вдали от критической точки v 2 67; 2 92; 4 95; 5 96; 9 92 см3 / г, показывают, что теплоемкость cv с увеличением температуры монотонно увеличивается, достигает некоторого своего максимального значения при определенной температуре, затем происходит скачкообразное ее уменьшение, что является признаком совершения перехода из двухфазного состояния в однофазное через пограничную кривую. В однофазной области в исследованном температурном интервале теплоемкость с на изохорах раствора данной концентрации с увеличением температуры монотонно уменьшается. Установлено, что величины теплоемкости сс в двухфазной области и их разрыв при переходе в однофазное состояние с ростом значения v возрастают.

Экспериментальное исследование изохорной теплоемкости некоторых углеводородов и спиртов.

Характер сингулярности изохорной теплоемкости одноком понентной жидкости таков, что до сих пор можно встретит утверждения, основанные на рассмотрении искаженного участ ка аномалии, об отсутствии расходимости этой величины в кри тической точке.

Уравнение для изохорной теплоемкости са записывается следующим образом ( г V сопз.

Следовательно, изохорную теплоемкость можно определить как количество теплоты, которое необходимо подвести к системе при постоянном объеме, чтобы повысить ее температуру на один градус.

Здесь Су — изохорная теплоемкость в идеальном состоянии, отнесенная к одной частице газа; Л, Л / — число положительных ионов и электронов.

Покажите, что изохорная теплоемкость этого газа не зависит от объема.

С г — изохорная теплоемкость газа; i CPICV; Pt и Р2 — начальное и конечное давление; СР — изобарная теплоемкость газа; TI и TZ — начальная и конечная температура; Vi и У2 — — начальный и конечный объем.

Зависимость изохорной теплоемкости от температуры для простых кристаллических веществ.| Изобарная теплоемкость металлов.

Таким образом, изохорная теплоемкость кристалла простого вещества должна быть равна 25 Дж / ( К-моль), Это правило соблюдается только при достаточно высоких температурах для многих металлов, начиная с четвертого периода системы элементов. Чем больше атомная масса элемента, тем при более низкой температуре достигается теоретическое значение теплоемкости. Теплоемкость алмаза не достигает этого значения даже при 1200 С.

Удельная теплоемкость: понятие и формула для расчета

Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:

Нагревание Q = cm(tконечная — tначальная) Охлаждение Q = cm(tначальная — tконечная) Q — количество теплоты c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса tконечная — конечная температура tначальная — начальная температура

В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.

С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:

Удельная теплоемкость вещества c= Q/m(tконечная — tначальная) Q — количество теплоты c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса tконечная — конечная температура tначальная — начальная температура

Также ее можно рассчитать через теплоемкость вещества:

Удельная теплоемкость вещества c= C/m c — удельная теплоемкость вещества [Дж/кг*˚C] C — теплоемкость вещества [Дж/˚C] m — масса

Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:

Количество теплоты, необходимое для нагревания тела Q = C(tконечная — tначальная) Q — количество теплоты c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса tконечная — конечная температура tначальная — начальная температура

Краткая теория и методика выполнения работы

Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:

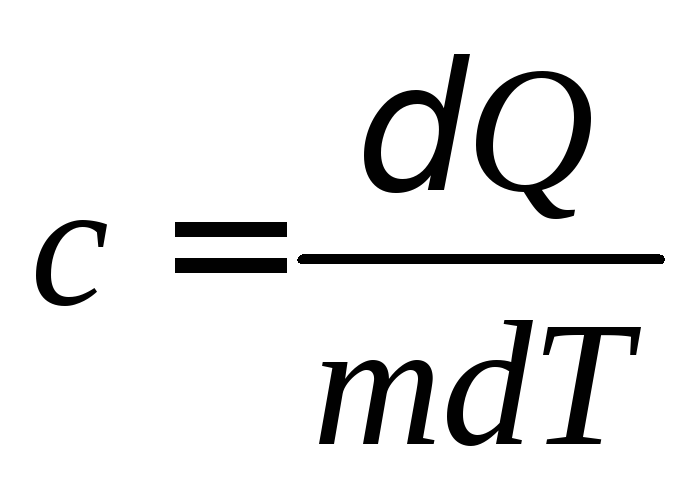. (4.1)

Теплоемкость
одного моля вещества называется молярной
теплоемкостью:

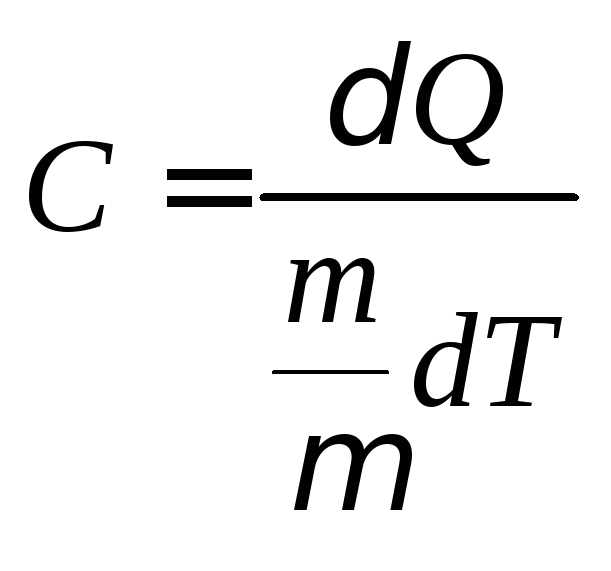, (4.2)

где
m – масса, µ – молярная масса вещества,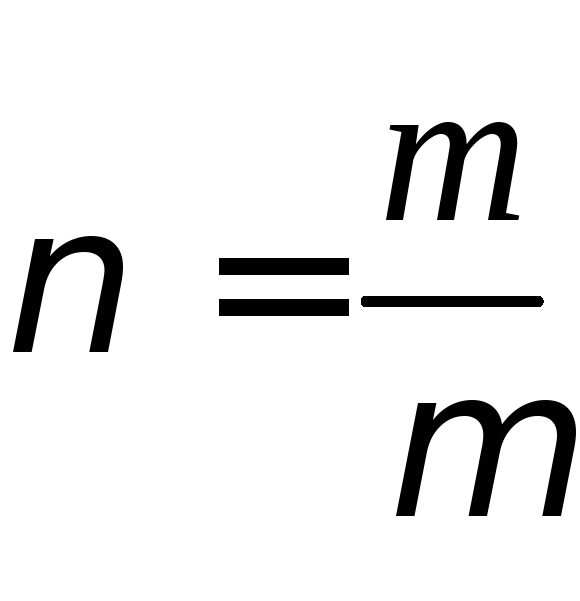– число молей газа.

Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,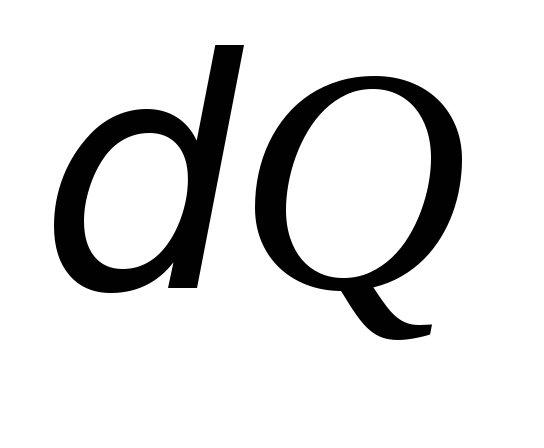
сообщенное системе, расходуется на
увеличение ее внутренней энергии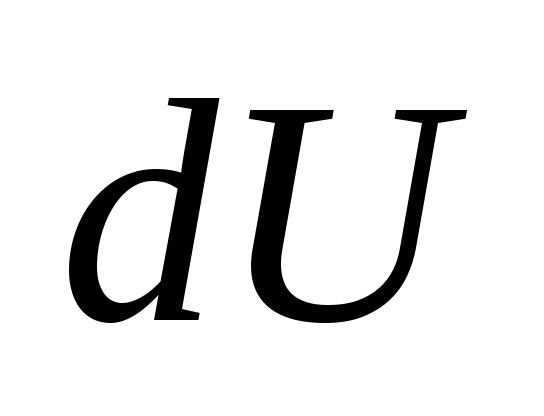и на совершение системой работы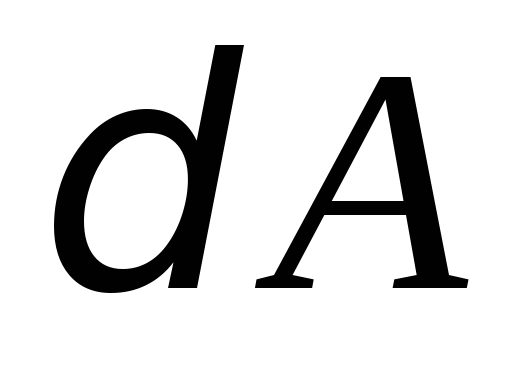против внешних сил:

. (4.3)

Изменение
внутренней энергии идеального газа в
случае изменения его температуры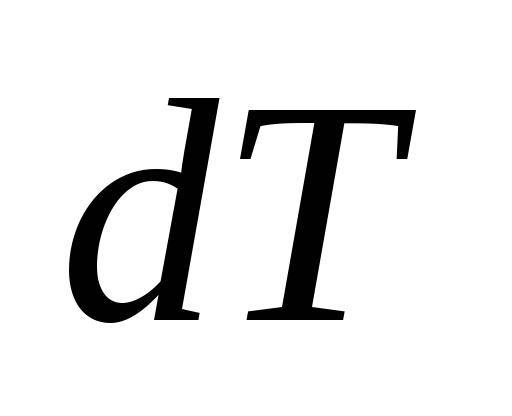равно:

, (4.4)

здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.

При
расширении газа система совершает
работу:

. (4.5)

Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:

. (4.6)

Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергии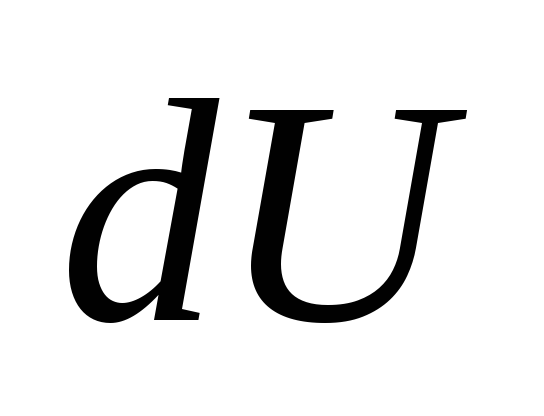и совершение газом работы:

.

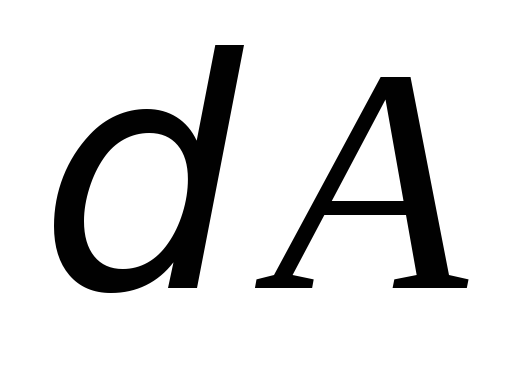Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:

. (4.7)

Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),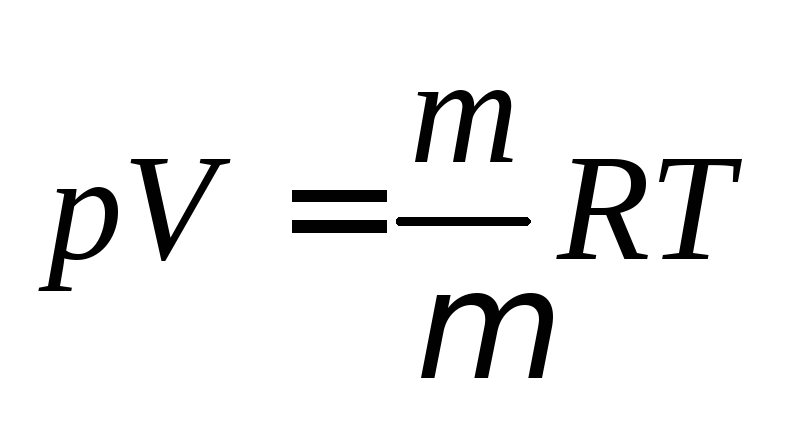
можно показать, что для одного моля газа
справедливо соотношение:

,

поэтому:

.

Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:

. (4.8)

Отношение
теплоемкостей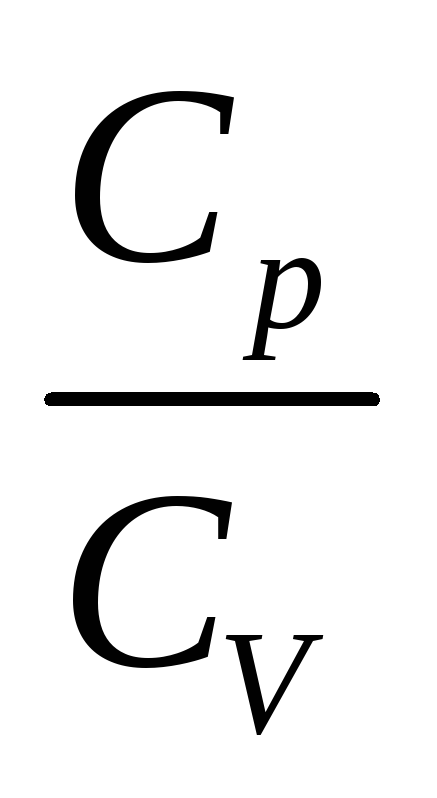обозначаюти называют показателем адиабаты или
коэффициентом Пуассона:

. (4.9)

Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.

На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.

Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:

. (4.10)

Продифференцировав
уравнение Клапейрона–Менделеева,
получим:

.

Выразим
из негои подставим в формулу (4.10):

.

Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:

.

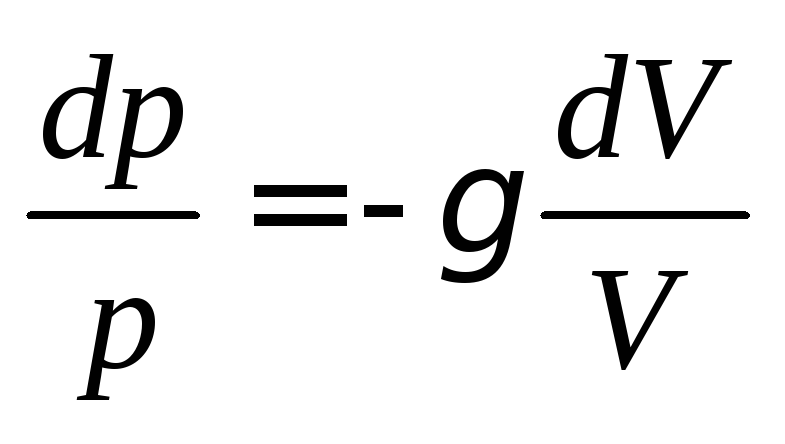Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:

.
(4.11)

Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.

Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме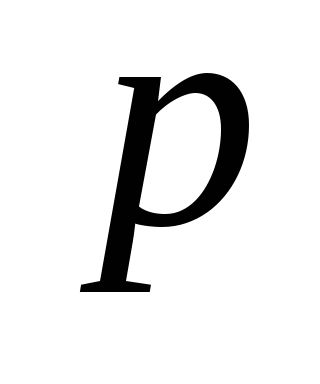–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.

Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,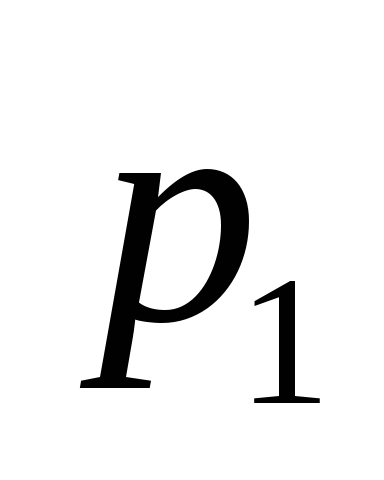
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.

Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.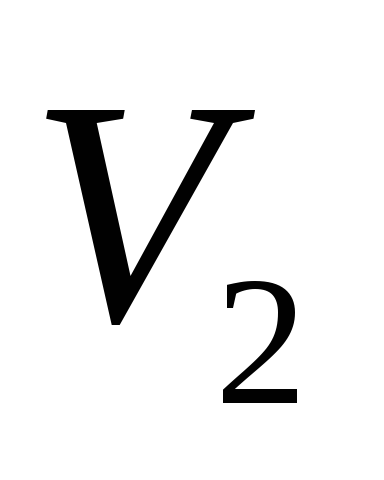
При этом температура воздуха, оставшегося
в сосуде, понизится до.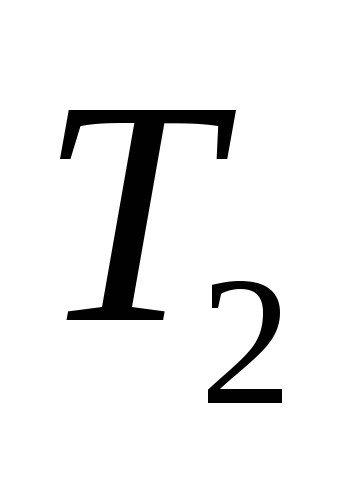
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):

или.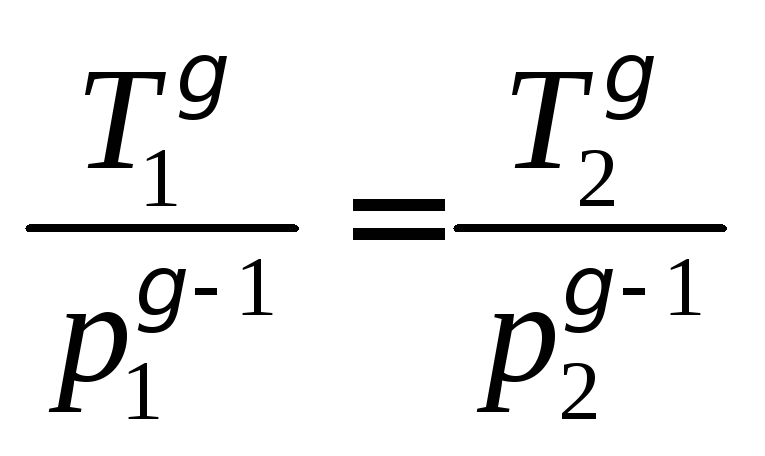

Отсюда:

. (4.12)

После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.

Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:

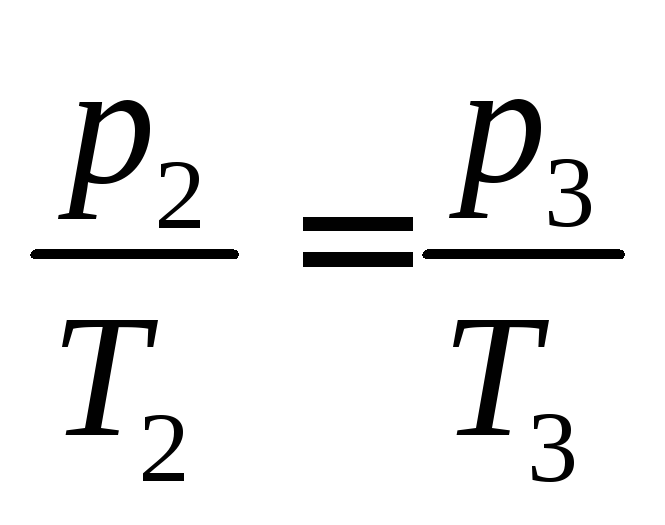или

. (4.13)

Из уравнений (4.12)
и (4.13) получим:

.

Прологарифмируем
это выражение:

.

Поскольку
избыточные давления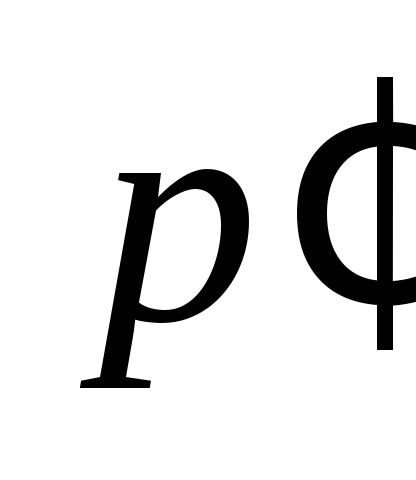и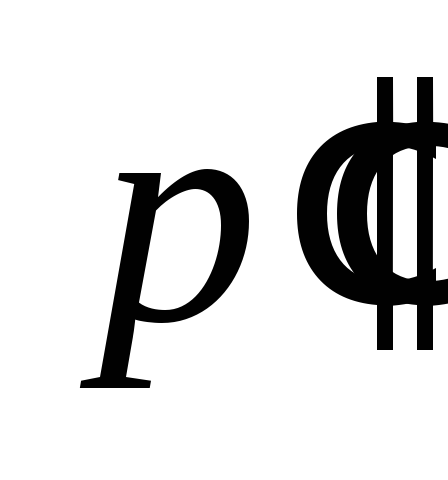очень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,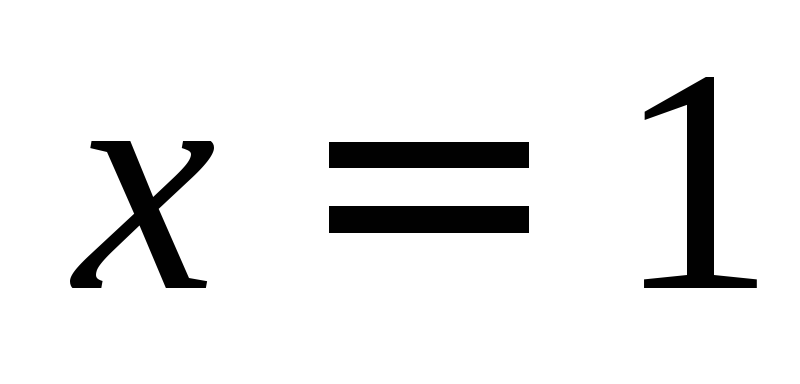
будем иметь:

.

Откуда:

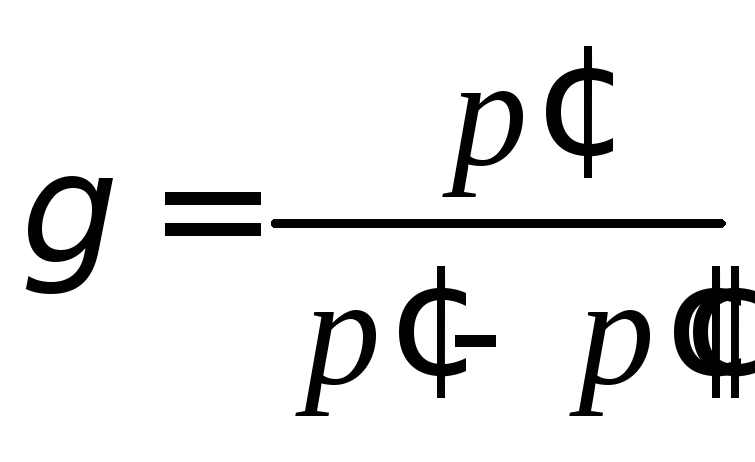. (4.14)

Избыточные
давления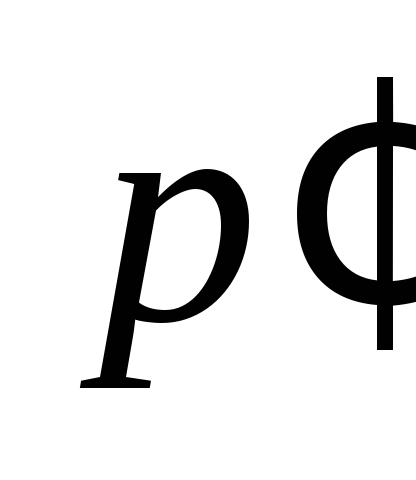и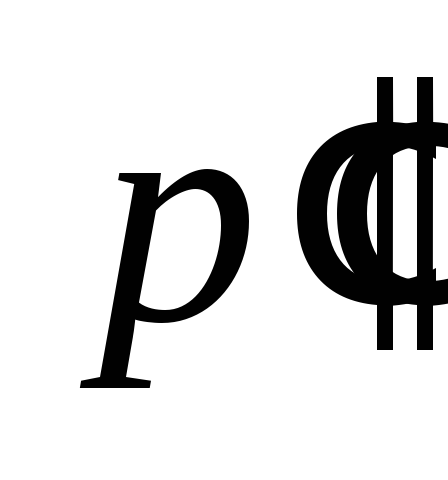измеряют с помощью дифференциального
датчика давления.

Удельная и молярная теплоёмкость[править | править код]

Молярная теплоёмкость — теплоёмкость 1 моля вещества :

CM=Cν=1νδQΔT,{\displaystyle C_{M}={\frac {C}{\nu }}={\frac {1}{\nu }}{\frac {\delta Q}{\Delta T}},}

где ν=mM,{\displaystyle \nu =m/M,} m{\displaystyle m} — масса, M{\displaystyle M} — молярная масса вещества.

Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К).

Формула расчёта удельной теплоёмкости:

c=CMM=δQmdT,{\displaystyle c={\frac {C_{M}}{M}}={\frac {\delta Q}{mdT}},}

где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.

2.1 Состав и классификация природных газов

Природные газы, добываемые из чисто газовых, нефтяных и газоконденсатных месторождений,
состоят из углеводородов гомоло­гического
ряда метана с общей формулой С_nН_2n+2. а также
неугле­водородных компонентов: азота (N₂),
углекислого газа (СО₂), се­роводорода (H₂S), благородных
(инертных) газов (гелия, аргона, криптона, ксенона), ртути.

Число углеродных атомов в
молекуле углеводородов п может достигать 17—40.

Метан (СН₄), этан (С₂Н₆) и этилен (С₂Н₄)
при нормальных ус­ловиях (р= 0,1 МПа и Т = 273 К)
являются реальными газами.

Пропан (С₃Н₈), пропилен (С₃Н₆),
изобутан (i-C₄H₁₀), нормальный бутан (п-С₄Н₁₀)
бутилены (С₄Н₈) при атмосферных условиях нахо­дятся в
парообразном (газообразном) состоянии, при повышенных давлениях—в жидком состоянии. Они входят в состав жидких (сжиженных)
углеводородных газов.

Углеводороды, начиная с изопентана (i-C₅H₁₂), при
атмосферных условиях нахо­дятся в жидком состоянии. Они входят в состав бензиновой
фрак­ции. Их называют углеводородным конденсатом. Углеводороды,
в молекулу которых входит 18 и более атомов углерода (от С₁₈Н₃₈),
расположенных в одну цепочку, при атмо­сферных условиях находятся в твердом состоянии.

Природные газы классифицируют потрем группам:

1)Газы, добываемые из чисто газовых месторождений.

2)Газы,
добываемые вместе с нефтью (попутные газы).

3)Газы, добываемые из газоконденсатных
месторождений.

Газовыми и
газоконденсатными месторождениями являются месторождения, которые находятся в
пластовых условиях в однофазном состоянии.Нефтяными
являются залежи, в которых объем нефтяной части залежи больше объема газовой
шапки и составляет более 0,75.Газонефтяные
0,5-0,75.Нефтегазовые
или нефтегазоконденсатные (НГКМ), в которых объем нефтяной части0,25-0,5. В газовых
игазоконденсатных месторождениях
содержание метана обычно превышает 90%, тогда как в газонефтяных находится в
пределах 50%.

Сухой газ состоит преимущественно из метана. Жирный газ
содержит в своем составе более тяжелые компоненты, характерен для попутных
нефтяных газов.Искусственными газами называют газы, полученные при сухой перегонке
твердых топлив (каменный уголь, горючий сланец).