Физические свойства жидкостей и газов

Как вычислить коэффициент

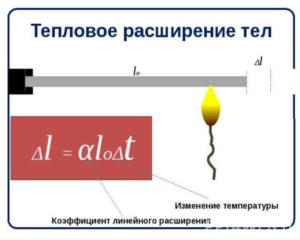Чтобы вычислить коэффициент, применяют инженерную формулу.

Для определения деформации в сантиметрах, необходимо знать коэффициент изменения, длину трубопроката. Рабочая температура равна комнатному значению.

Первым делом определяют разницу температуры, далее умножают на показатель длины. Коэффициент умножают на получившуюся цифру.

Пример расчета:

Во время вычислений получился коэффициент равный двадцати миллиметрам. Значит, в сантиметрах изменение будет равно двум. Во время укладки сети этот показатель необходимо учитывать.

Как компенсировать получившиеся сантиметры:

1.укладывать сеть, применяя прямые углы. С одной стороны трубы, лучше сзади, оставляют зазор, чтобы было место для деформации. Как правило, трубы отклоняются, образуя острый угол.

2.в сеть монтируют компенсаторы в форме петли.

3.укладывают трубы в виде буквы П, стыкуя скользящую опору с недвижимой. Так понижается расширение.

Формула жидкости

Страницы:| 01 |

Многочисленные формулы предлагались изобретательными исследователями многие годы, и каждая формула имела свои преимущества и недостатки. Следующие 6 формул (таблица 1) выбраны, чтобы проиллюстрировать эволюцию концепции инфузионной терапии у детей с ожогами. Первые три формулы теперь имеют историческое значение, а остальные три использовались в настоящее время. В приложении дается более полный список формул.

Коуп и Мур (1947) были первыми, кто начали составлять формулу. Они первыми попытались сопоставить какое количество жидкости требуется на площадь ожоговой поверхности и дали убедительные подтверждения тому, сколько жидкостей нужно перелить больному в первые 48 часов. С годами они обнаружили, что их больные бывают перегружены жидкостью, поэтому максимально рекомендовали, расход жидкостей от 10 — 12 % веса тела в литрах жидкости.

Эванс (1952) разработал свою формулу используя данные Коупа и Мура, на основе состава жидкости ожоговых волдырей. Кроме этого он давал дневное количество жидкостей и ограничивал максимум жидкости, даваемой на ожог, который рассчитывался исходя из 50 % ожоговой поверхности.

Реисс (1953) работая в Военном госпитале ожогового отделения в Бруке, используя формулу Эванса в первые 48 часов, наполовину. Впоследствии ожоговое отделение в Бруке (Пруитт, 1970) исключило назначения коллоидных растворов в первые 24 часа, используя только один раствор Рингер лактата.

Бакстер (1968) предложил инфузионную терапию, используя большое количество только Рингер лактата, измеряя диурез и оценивая клиническое состояние, в первые 24 часа. Он добавлял коллоид в течение первых суток. Опыт показал, что эта формула может использоваться во многих случаях. Проблемы появляются когда ребенка перегружают жидкостью, дают слишком много жидкости сильно обожженному больному.

Карвагал (1975) считает, что введение жидкостей должно быть основано исключительно на расчете поверхности тела. Его формула, в которой используется один раствор, требует 2-х рассчетов: один — процент поверхности ожогов — ожоговое содержание; и другой расчет основан на общей площади поверхности тела — физиологическая потребность. Он рекоммендует раннее применение коллоида (альбумина) и считает, что формула имеет особые преимущества для ожоговых больных всех возрастов и с разной степенью ожога

При использовании этой формулы важно аккуратно вести оценку площади поверхности тела

Боусер и Колдуелл (1983) отстаивает применение гипертонического раствора для реанимации, особенно у детей с ожогами. Они считают, что при таком режиме избегается перегрузка жидкостью, и восстанавливаются потерянные ионы натрия. Поддержка нормальной осмолярности сыворотки и отношение нормальной внутриклеточной жидкости к экстра-клеточной считается преимуществом. Использование гипертонической жидкости для реанимации детей требует постоянного мониторинга за больным, чтобы избежать гипернатремии, гипертонических синдромов и возможных синдромов центральной нервной системы. Никаких коллоидов в первые 48 часов не применялось.

Аэродинамика

Сжимаемость — важный фактор аэродинамики . На низких скоростях сжимаемость воздуха не имеет значения по сравнению с конструкцией самолета , но по мере того, как воздушный поток приближается к скорости звука и превышает ее, в конструкции самолета становится важным множество новых аэродинамических эффектов. Эти эффекты, часто по несколько одновременно, сильно затрудняли достижение самолетами эпохи Второй мировой войны скоростей, намного превышающих 800 км / ч (500 миль / ч).

Многие эффекты часто упоминаются вместе с термином «сжимаемость», но обычно имеют мало общего со сжимаемостью воздуха. С чисто аэродинамической точки зрения этот термин должен относиться только к тем побочным эффектам, которые возникают в результате изменений воздушного потока от несжимаемой жидкости (по действию схожей с водой) на сжимаемую жидкость (действующую как газ) в качестве газа. скорость звука приближается. В частности, есть два эффекта: волновое сопротивление и критическая маш .

Одно осложнение возникает в гиперзвуковой аэродинамике, где диссоциация вызывает увеличение «условного» молярного объема, потому что моль кислорода, как O ₂ , становится 2 молями одноатомного кислорода, а N ₂ аналогично диссоциирует до 2 N. Поскольку это происходит динамически, как воздух. Обтекает аэрокосмический объект, удобнее изменять коэффициент сжимаемости Z , определенный для начальных 30 грамм-моль воздуха, а не отслеживать изменяющуюся среднюю молекулярную массу миллисекунду за миллисекундой. Этот зависимый от давления переход происходит для атмосферного кислорода в диапазоне температур 2 500–4 000 К и в диапазоне 5 000–10 000 К для азота.

В переходных областях, где эта зависящая от давления диссоциация является неполной, значительно возрастают как бета (отношение перепада объема / давления), так и дифференциальная теплоемкость при постоянном давлении. При умеренном давлении, выше 10 000 К, газ далее диссоциирует на свободные электроны и ионы. Z для образовавшейся плазмы можно аналогичным образом вычислить для моля исходного воздуха, получив значения от 2 до 4 для частично или однократно ионизированного газа. Каждая диссоциация поглощает много энергии в обратимом процессе, и это значительно снижает термодинамическую температуру гиперзвукового газа, замедленного вблизи аэрокосмического объекта. Ионы или свободные радикалы, переносимые на поверхность объекта путем диффузии, могут высвободить эту дополнительную (нетепловую) энергию, если поверхность катализирует более медленный процесс рекомбинации.

8.2 Реальный газ

Относительнуюплотностьреальногогазавычисляютпоформуле

где

d (t, р) -относительнаяплотностьреальногогаза;

Z_air(t, p) -коэффициентсжимаемостисухоговоздухастандартногосостава;

Z_mix(t, p) -коэффициентсжимаемостигаза.

КоэффициентсжимаемостиZ_mix(t, p) вычисляютпоформуле (), сиспользованиемзначенийкоэффициентовсуммирования , приведенныхдляиндивидуальныхчистыхвеществв (). КоэффициентсжимаемостиZ_air(t, p) приведенв ():

Z_air (273,15 К, 101,325 кПа) = 0,99941;

Z_air (288,15 К, 101,325 кПа) = 0,99958;

Z_air (293,15 К, 101,325 кПа) = 0,99963.

Плотностьреальногогазавычисляютпоформуле

где

ρ (t, p) -плотностьреальногогаза.

ЧислоВоббереальногогазавычисляютпоформуле

где

W-числоВоббереальногогаза;

-вычисляютпоформуле ().

Примечание 16 -Требуетсяопределеннаявнимательностьприпримененииединицизмеренияпри
вычислениях, приведенныхвнастоящемподразделе, особеннопривычисленияхплотности. ПриR, выраженнойв джоуляхнамоль-кельвин, р-вкилопаскаляхиМ-вкилограммахнакиломоль, значениеρавтоматическиполучаетсявкилограммахнакубическийметр-эторекомендуемаяединицаСИ.

Рекомендации

1. ^
2. Цукер, Роберт Д.; Библарц, Оскар (2002). Основы газовой динамики (2-е изд.). Wiley Books. ISBN 0-471-05967-6. стр. 327
3. McQuarrie, Donald A .; Саймон, Джон Д. (1999). Молекулярная термодинамика. Книги университетских наук. ISBN 1-891389-05-X. стр.55
4. Y.V.C. Рао (1997). Химическая инженерия термодинамика. Universities Press (Индия). ISBN 81-7371-048-1.
5. Cengel, Yunus A .; Болес, Майкл А. (2015). Термодинамика: инженерный подход, восьмое издание. McGraw-Hill Education. ISBN 978-0-07-339817-4. стр.140
6. Cengel, Yunus A .; Болес, Майкл А. (2015). Термодинамика: инженерный подход, восьмое издание. McGraw-Hill Education. ISBN 978-0-07-339817-4. стр.139
7. Smith, J.M .; и другие. (2005). Введение в термодинамику химической инженерии (Седьмое изд.). Макгроу Хилл. ISBN 0-07-310445-0. page73
8. (6 изд.). MCGraw-Hill. 1984 г. ISBN 0-07-049479-7. стр. 3-268

4.1 Энтальпия сгорания

Наиболееважнымифундаментальнымифизическимивеличинами, необходимымипривычислениизначенийтеплотысгорания, исходяизпринципа, положенноговосновуметода, являются (стандартные) молярныеэнтальпиисгораниядляидеальныхгазов-компонентовсмеси. Этивеличины
являютсясложнымифункциямитемпературы; следовательно, необходимыезначениязависятотстандартнойтемпературысгоранияt1. Попрактическимсоображениямпредполагается, чтосампользовательневыполняетрасчеты, которыедаютсоответствующиезначениямолярнойэнтальпиисгорания
прилюбойпроизвольнойстандартнойтемпературе. Вместоэтогоприводятсятаблицыдлятемпературы
t1 =25°С, 20°С, 15°Си°С

В () рассматриваютсяметодыполучения
табличныхзначений; важноотметить, чтовсе 4 значениядлялюбоговеществатермодинамически
взаимосвязаны

Длязначениятеплотысгорания, рассчитанногополюбомуизтрехвозможныхвариантов, впринципе, требуетсятакназываемаяэнтальпийнаяпоправкадлятого, чтобыпересчитатьэнтальпиюидеальногогазаприсгораниигазовойсмесивзначение, соответствующеереальномугазу. Однакоона
обычнонастолькомала, чтоеюможнопренебречь. Обоснование, подтверждающееэто, приведенов ().

Показатели сжимаемости грунта

Характеристики почвы на деформацию определяются двумя методами:

1. В жестких, не поддающихся растяжению, компрессионных устройствах. В них полностью исключается боковое расширение.
2. В условиях возможного бокового расширения.

Степень сжатия периодически увеличивают, после каждой нагрузке дают время на стихание процесса деформации. После стабилизации измеряют осадку и выводят компрессионную кривую.

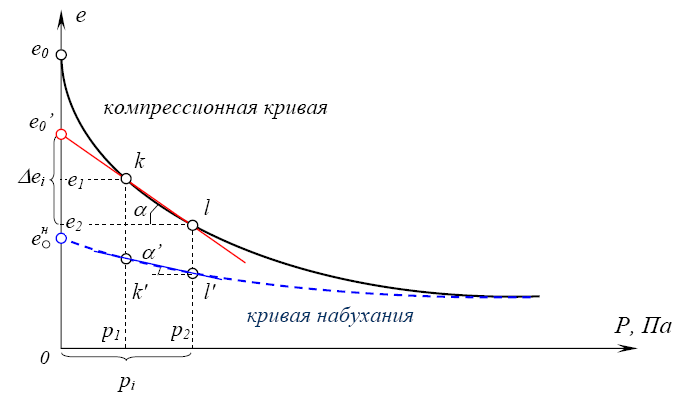
К показателям деформирования породы относят:

• коэффициент сжимаемости;
• относительной сжимаемости;
• модуль деформации;
• структурную прочность.

Коэффициент сжимаемости

Первый показатель, изменение рыхлости породы под давлением, крайне важен. Он определяет зависимость конечного деформирования почвенной смеси от давления и дает возможность установить формат осадка основания строения.

Коэффициент относительной сжимаемости

Это параметр деформации относительно единицы давления. При определении этого показателя учитывают: усадку образца под разным нажимом от 0 до p1, начальную высоту исследуемого материала в мм и уровень пористости.

Коэффициент сжимаемости, m0, связан с модулем поперечной деформации E0 (упругости). Степень поперечного расширения для разных песков, супесей, суглинков, глин, отличается.

Выделяют три категории грунта:

1. сильно сжимаемый – m > 0,5 (МПа)-1
2. средне сжимаемый – 0,1>m > 0,5 (МПа)-1
3. мало сжимаемый – m < 0,5 (МПа)-1

Модуль упругости

Эта величина переменная. Она меняется: от степени сдавливания, времени воздействия, плотности породы, площади штампа. Чтобы спрогнозировать поведение почвенного слоя в условиях сдавливания, необходимо знать эти показатели.

Структурная прочность

Степень уплотнения зависит от структуры почвы, рыхлости, наличия кристаллизационных связей. Структурная прочность – это параметр напряженности, при котором происходит разрушение связей. Небольшие нагрузки вызывают легкую деформацию, при этом коэффициент пористости практически остается неизменным. При усилении нагрузок и достижении структурной прочности происходит перекомпоновка частиц, уплотнение и уменьшение пористости.

Коэффициент — объемное сжатие

Знак минус поставлен для того, чтобы коэффициент объемного сжатия жидкости был положительной величиной. В самом деле, при увеличении давления ( dp 0) объем жидкости уменьшается ( dVx 0) и наоборот, то есть дифференциалы в числителе и знаменателе равенства (19.22) имеют разные знаки. Коэффициент объемного сжатия жидкости обычно считается универсальной постоянной, то есть считается, что он не зависит ни от температуры, ни от давления, но для разных жидкостей он принимает разные значения.
 

При нагревании такого сосуда вследствие очень малого значения коэффициента объемного сжатия жидкого хлора в нем резко возрастает давление, которое во много раз превышает расчетное. Резкий рост давления внутри сосуда является причиной гидравлического разрыва его обечайки и других конструктивных элементов. Происходит выброс хлора в атмосферу и отравление людей.
 

Объемная деформация воды под действием сил давления характеризуется коэффициентом объемного сжатия pw 5 — 10 — 8 для давлений 1 — 500 am и коэффициентом температурного расширения рг: ( 14 -: — 719) 10 — 6 для интервала температур 0 ч — 100 С. Поэтому при рассмотрении движения воды в трещиноватой среде для обычно встречающихся в инженерной практике колебаний давлений и температур изменяемость объема воды весьма мала; и ею практически можно пренебречь.
 

Нельзя, однако, изменить характер зависимости, например, коэффициента объемного сжатия ( при постоянной температуре) от давления, изменяя единицы, в которых измеряются объем и давление. Если этот коэффициент уменьшается с увеличением давления при одном каком-нибудь выборе единиц, то он будет уменьшаться и при любом другом выборе их. Тогда надо ответить на вопрос, возникший фактически с момента изобретения термометра Галилеем: чем отличается измерение температуры от измерения такой величины, как, например, объем.
 

Модулем объемной упругости жидкости / С называется величина, обратная коэффициенту объемного сжатия.
 

Очевидно, что модуль объемной упругости — К является обратной величиной коэффициента объемного сжатия.
 

Винтовой пресс Рухгольца для тарировки пружинных манометров работает на масле с коэффициентом объемного сжатия р 6 25 10 — 5 см2 / кг.
 

Величина получаемых давлений пропорциональна мощности, обратно пропорциональна длительности импульса и зависит от коэффициента объемного сжатия жидкости. Средой для получения электрогидравлического эффекта может служить любая жидкость; наиболее удобной является техническая вода.
 

Найти приближенное значение частоты со первого тона вертикальных колебаний жидкости в трубе, если коэффициент объемного сжатия последней равен / ill / M J, а труба имеет круговое поперечное сечение площадью S. Считать, что амплитуды перемещений частиц жидкости по вертикали и изменяются но линейному закону ( смотри зпюру), растеканием жидкости в радиальном направлении пренебречь.
 

Поскольку непосредственное измерение сжимаемости жидкости в процессе испытаний затруднительно, НАТИ предложил методику определения коэффициента объемного сжатия по результатам специальных экспериментов. Так, при испытании гидромотора объем жидкости в под-поршневом пространстве, сжатый до рабочего давления, в конце рабочего хода поршня подключается к сливной магистрали с низким давлением и расширяется.
 

Здесь Ь, у-структурные параметры породы, зависящие от коэффициентов Юнга и Пуассона, коэффициентов объемного сжатия кварца и цемента породы, объемного содержания кварца и цемента породы, коэффициента пористости на контуре пласта; р, рк — текущее и контурное давление соответственно; kK — коэффициент проницаемости внешней границы.
 

Сжимаемостью называют способность жидкости изменять свою плотность при изменении давления или температуры; она характеризуется коэффициентом объемного сжатия Э1 / ( / Ср 273) ijepad. Если плотность при движении жидкости или газа не изменяется, то жидкость называют несжимаемой.
 

Для некоторых материалов, например глины, при деформации всестороннего сжатия между сжимающим давлением р и коэффициентом объемного сжатия 0 — div w также получается аналогичная зависимость.
 

Физически коэффициент объемного расширения fip показывает относительное изменение объема при изменении температуры на 1 С, а коэффициент объемного сжатия 3СЖ — относительное изменение объема при изменении давления на 0 1 МПа.
 

Относительное изменение объема жидкости при увеличении давления на 1 кг на каждый квадратный сантиметр ее поверхности характеризуется коэффициентом объемного сжатия ри.
 

Основные физические свойства жидкостей

В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.

Жидкости подразделяют на два вида: капельные и газообразные. Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами). Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию. К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие, а к газообразным — все газы.

Гидравлика изучает капельные жидкости. При решении практических задач гидравлики часто пользуются понятием идеальной жидкости — несжимаемой среды, не обладающей внутренним трением между отдельными частицами.

К основным физическим свойствам жидкости относятся плотность, давление, сжимаемость, температурное расширение, вязкость.

Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.

Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.

Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях.

Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.

В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.

Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.

ЧОсновы гидростатикиПонятие о гидравлике

Капиллярные явления. Формула Жюрена

В жизни часто приходится иметь дело с телами, пронизанными множеством мелких каналов (бумага, пряжа, кожа, почва, дерево). Приходя в соприкосновение с водой или другими жидкостями, такие тела очень часто впитывают в себя жидкость. На этом основано действие полотенца, фитиля в лампе, питание растений. Подобные явления можно также наблюдать в очень узких стеклянных трубочках, которые называются капиллярными (от латинского слова «капилля» – волос).

Для капиллярных сосудов характерна прежде всего кривизна поверхности жидкости в них, поэтому в таких сосудах в полной мере проявляются эффекты, обусловленные избыточным давлением Лапласа. К числу таких эффектов относится капиллярный подъем.

Рис. 6.17

Найдем высоту поднятия жидкости в цилиндрической капиллярной трубочке радиуса r
(рис. 6.17а). Пусть жидкость смачивает поверхность трубочки, вследствие чего в последней
образуется симметричный вогнутый мениск с радиусами кривизны двух взаимно перпендикулярных
сечений . Отметим еще, что изменением давления
жидкости при ее поднятии на высоту порядка r будем пренебрегать. В этом приближении
давление во всех точках мениска можно считать одинаковым.

Под искривленной поверхностью вогнутого мениска давление в жидкости, как это было рассмотрено
выше, меньше атмосферного давления Р на величину давления
Лапласа (рис. 6.17б).

Под действием возникшей разности давлений на уровне поверхности жидкости в широком сосуде и непосредственно под мениском в капиллярной трубочке жидкость начинает подниматься по трубочке, и будет подниматься до тех пор, пока гидростатическое давление поднявшегося столба жидкости не будет равно давлению Лапласа.

Условие равновесия жидкости в капиллярной трубочке определяется равенством

.

(6.23)

где ρ – плотность жидкости,h – высота ее поднятия в трубочке,g – ускорение силы тяжести.

Из (6.23) следует:

.

(6.24)

Преобразуем (6.24), выразив радиус кривизны R мениска через радиус капиллярной
трубочки r (рис. 6.18).

Из рис. 6.18 следует, что

.

(6.25)

Подставляя (6.25) в (6.24), получаем:

.

(6.26)

Рис. 6.18

Полученная формула, определяющая высоту поднятия жидкости в капиллярной трубочке, носит название формулы Жюрена. Очевидно, что чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость. Кроме того, высота поднятия растет с увеличением коэффициента поверхностного натяжения жидкости.

В частном случае для жидкости, полностью смачивающей стенки капилляра , формула Жюрена принимает вид:

.

(6.27)

Рис. 6.19

Капиллярный подъем может наблюдаться не только в цилиндрических капиллярах. Жидкость
поднимается и между двумя пластинами, разделенными узким зазором (рис. 6.19). Если пластины
параллельны друг другу, то мениск имеет цилиндрическую форму с радиусом кривизны одного
из сечений, равным . Радиус кривизны другого нормального сечения цилиндрического мениска можно считать равным бесконечности. При этом условии высота поднятия жидкости между пластинами равна:

.

(6.28)

В формуле учтено, что давление Лапласа при цилиндрическом мениске равно .

Если жидкость не смачивает капилляр, то в трубочке образуется выпуклый мениск, центр кривизны которого не вне, а внутри жидкости. В этом случае добавочное давление Лапласа направлено вниз. Уровень жидкости в капиллярной трубочке опускается ниже уровня жидкости в широкой части сосуда. Говорят, что имеет место отрицательный капиллярный подъем (рис. 6.20). Отметим еще, что формула Жюрена может быть использована для экспериментального определения коэффициента поверхностного натяжения жидкости. Для этого нужно измерить радиус капиллярной трубочки и высоту поднятия в ней жидкости.

Рис. 6.20

В заключение подчеркнем, что явления, обусловленные капиллярностью, играют большую роль в природе, особенно велико их значение в живых организмах, значительная часть кровеносной системы которых представляет собой мельчайшие капилляры.

Растворимость газов

Многие жидкости способны растворять в себе газы. Эта способность характеризуется количеством растворенного газа в единице объема жидкости, различается для разных жидкостей и изменяется с увеличением давления.

Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, то есть:

Vг	= k·	p
Vж	p

где V_г — объем растворенного газа, приведенный к нормальным условиям (p, Т);V_ж — объем жидкости;k — коэффициент растворимости;р — давление жидкости.

Коэффициент k имеет следующие значения при 20°С:

вода	0,016
керосин	0,13
минеральные масла	0,08
жидкость АМГ-10	0,1

При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказывается на работе гидросистем.

Давление — физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности. Для обозначения давления обычно используется символ p — от лат.pressura (давление).

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Приборы для определения сжимаемости

Исследования и определение вида грунта проводятся с помощью компрессионных приборов, одометров.

По результатам бокового давления, объему выделенной жидкости в водонасыщенных почвах определяют: коэффициент уплотнения, модуль деформации, структурную прочность.

Второй прибор, определяющий степень деформации, – стабилометр. Устройство представляет собой цилиндрическую камеру. Различают стабилометры с вертикальной или горизонтальной нагрузкой.

Минус лабораторных исследований в том, что нарастание давления в приборах происходит быстрее, чем в естественной среде. Это дает несколько завышенные показатели.

Экспериментальные значения

Крайне трудно сделать обобщение, при каких давлениях или температурах отклонение от идеального газа становится важным. Как показывает практика, закон идеального газа достаточно точен до давления около 2 атм и даже выше для небольших неассоциированных молекул. Например, метилхлорид , молекула с высокой полярностью и, следовательно, со значительными межмолекулярными силами, экспериментальное значение коэффициента сжимаемости находится при давлении 10 атм и температуре 100 ° C. Для воздуха (небольшие неполярные молекулы) примерно в тех же условиях коэффициент сжимаемости равен только (см. Таблицу ниже для 10 бар , 400 K).
Zзнак равно0,9152{\ displaystyle Z = 0,9152}Zзнак равно1,0025{\ displaystyle Z = 1,0025}

Сжимаемость воздуха

Нормальный воздух содержит в неочищенном виде 80 процентов азота N.₂и 20 процентов кислорода O₂. Обе молекулы маленькие и неполярные (и поэтому не связываются). Таким образом, можно ожидать, что поведение воздуха в широком диапазоне температур и давлений может быть приближено к идеальному газу с разумной точностью. Это подтверждают экспериментальные значения коэффициента сжимаемости.

Коэффициент сжимаемости воздуха (экспериментальные значения)

Температура (K)	Давление, абсолютное (бар)
1	5	10	20	40	60	80	100	150	200	250	300	400	500
75	0,0052	0,0260	0,0519	0,1036	0,2063	0,3082	0,4094	0,5099	0,7581	1.0125
80		0,0250	0,0499	0,0995	0,1981	0,2958	0,3927	0,4887	0,7258	0,9588	1,1931	1,4139
90	0,9764	0,0236	0,0453	0,0940	0,1866	0,2781	0,3686	0,4681	0,6779	0,8929	1,1098	1,3110	1,7161	2,1105
100	0,9797	0,8872	0,0453	0,0900	0,1782	0,2635	0,3498	0,4337	0,6386	0,8377	1,0395	1,2227	1,5937	1,9536
120	0,9880	0,9373	0,8860	0,6730	0,1778	0,2557	0,3371	0,4132	0,5964	0,7720	0,9530	1,1076	1,5091	1,7366
140	0,9927	0,9614	0,9205	0,8297	0,5856	0,3313	0,3737	0,4340	0,5909	0,7699	0,9114	1,0393	1,3202	1,5903
160	0,9951	0,9748	0,9489	0,8954	0,7803	0,6603	0,5696	0,5489	0,6340	0,7564	0,8840	1.0105	1,2585	1,4970
180	0,9967	0,9832	0,9660	0,9314	0,8625	0,7977	0,7432	0,7084	0,7180	0,7986	0,9000	1,0068	1,2232	1,4361
200	0,9978	0,9886	0,9767	0,9539	0,9100	0,8701	0,8374	0,8142	0,8061	0,8549	0,9311	1.0185	1,2054	1,3944
250	0,9992	0,9957	0,9911	0,9822	0,9671	0,9549	0,9463	0,9411	0,9450	0,9713	1,0152	1,0702	1,1990	1,3392
300	0,9999	0,9987	0,9974	0,9950	0,9917	0,9901	0,9903	0,9930	1,0074	1,0326	1,0669	1,1089	1,2073	1,3163
350	1,0000	1.0002	1.0004	1,0014	1,0038	1,0075	1.0121	1.0183	1,0377	1,0635	1.0947	1,1303	1,2116	1,3015
400	1.0002	1,0012	1,0025	1,0046	1.0100	1,0159	1.0229	1.0312	1,0533	1,0795	1,1087	1,1411	1,2117	1,2890
450	1.0003	1,0016	1,0034	1,0063	1,0133	1.0210	1,0287	1,0374	1,0614	1.0913	1,1183	1,1463	1,2090	1,2778
500	1.0003	1,0020	1,0034	1,0074	1,0151	1.0234	1.0323	1,0410	1.0650	1.0913	1,1183	1,1463	1,2051	1,2667
600	1.0004	1,0022	1,0039	1,0081	1,0164	1.0253	1.0340	1,0434	1,0678	1.0920	1,1172	1,1427	1,1947	1,2475
800	1.0004	1,0020	1,0038	1,0077	1,0157	1.0240	1.0321	1.0408	1,0621	1,0844	1,1061	1,1283	1,1720	1,2150
1000	1.0004	1,0018	1,0037	1,0068	1,0142	1.0215	1.0290	1.0365	1,0556	1,0744	1.0948	1,1131	1,1515	1,1889

Z{\ displaystyle Z}значения рассчитываются на основе значений давления, объема (или плотности) и температуры в Вассермане, Казавчинском и Рабиновиче, «Теплофизические свойства воздуха и компонентов воздуха»; Москва, Наука, 1966, и NBS-NSF Trans. TT 70-50095, 1971: и Вассерман и Рабинович, «Теплофизические свойства жидкого воздуха и его компонентов», Москва, 1968, и NBS-NSF Trans. 69-55092, 1970. .

Фугитивность

Фугитивность — это давление реального
газа, свойства которого выражены
уравнением состояния идеального газа.
Фугитивностью пользуются при расчетах
равновесных паровой и жидкой фаз и
числовых значений констант фазового
равновесия.

Для равновесной
системы, согласно законам Рауля и
Дальтона,

(34)

откуда

гдеР
— давление насыщенных паров чистого
компонента, Па; х’
— мольная концентрация компонента в
жидкой фазе, %, мол; П
— давление в системе, Па; у’
— мольная концентрация компонента в
паровой фазе, %, мол; k
— константа фазового равновесия
(Приложения
10 и 11).

Для
идеальной системы значение k
равно отношению давления насыщенных
паров данного компонента к давлению в
системе и характеризует распределение
данного компонента между паровой и
жидкой фазами. Для реальных систем
константа фазового равновесия, вычисленная
этим методом, не дает вполне
удовлетворительных результатов.

Для
реальных газов и растворов давление
насыщенных паров Р
и давление в системе П
заменяют соответственно фугитивностью
жидкости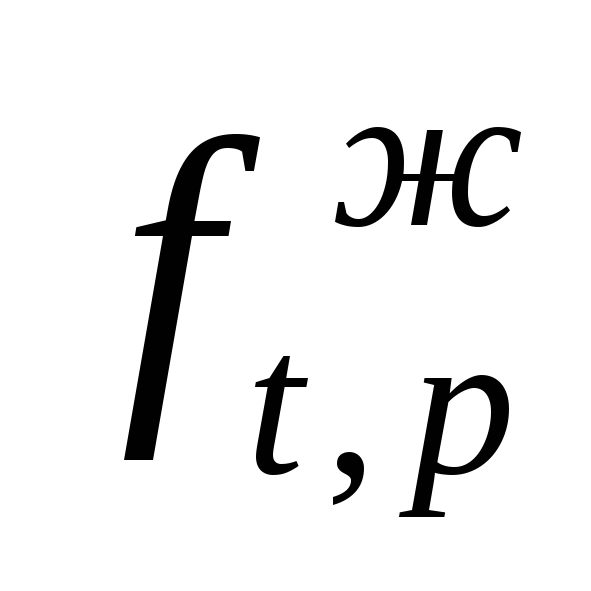
и паров .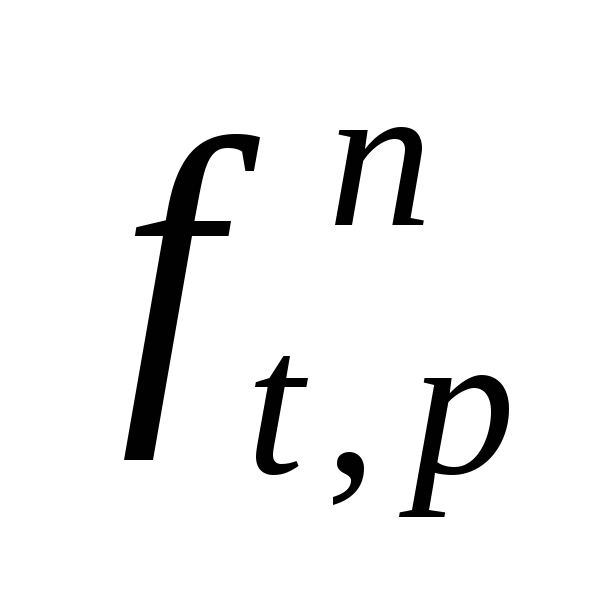
Уравнение (34) приобретает вид

а константа фазового
равновесия равна

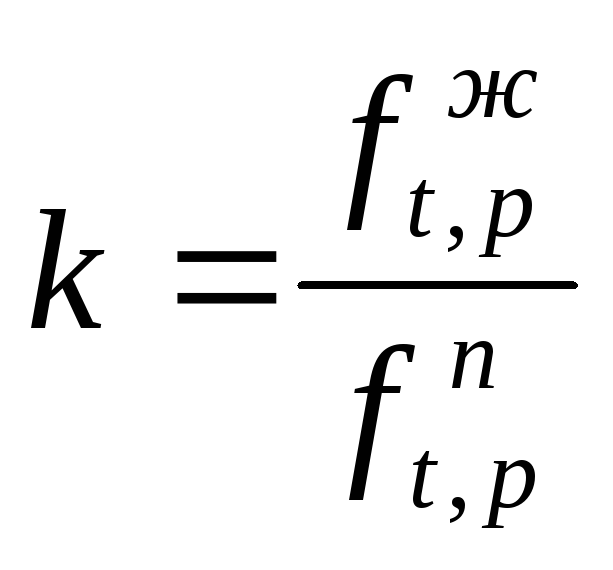(35)

Фугитивность
характеризует степень отклонения
свойств реального газа от идеального
в случае изотермического процесса. При
низких давлениях и высоких температурах
реальный газ приближается к состоянию
идеального газа, а величина f
— к величине Р.
Фугитивность имеет ту же размерность,
что и давление. Отношение фугитивности
к давлению называется коэффициентом
активности

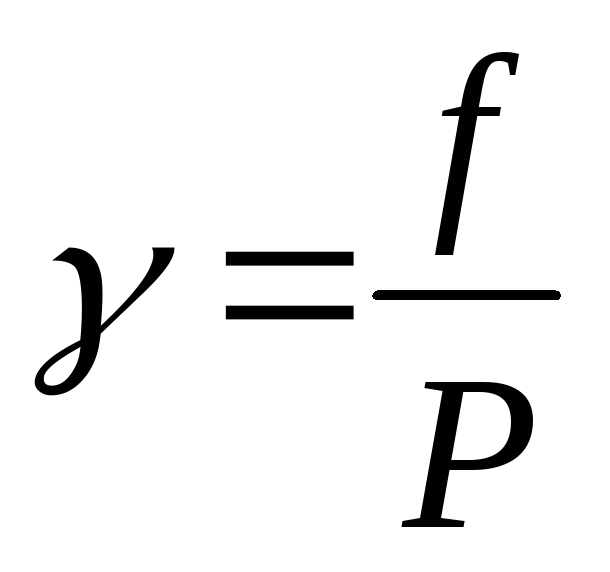(36)

Для
идеального газа .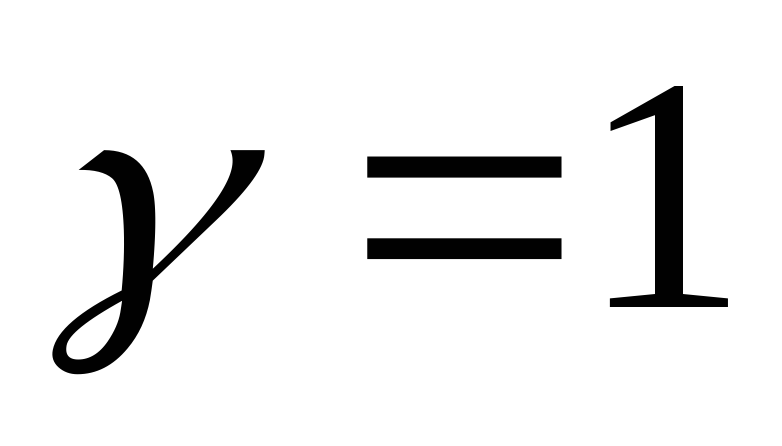

Установлено,
что коэффициент активности является
функцией приведенных температуры и
давления. Поэтому значение фугитивности
можно определить, пользуясь графиком
(рис. 9). По приведенной температуре Т_при приведенному
давлению Р_пр
находят коэффициент активности. Затем,
подставляя в уравнение (36) давление
насыщенных паров Р
или давление системы П,
получают соответственно фугитивность
жидкости или паров.

Для
точных расчетов константы фазового
равновесия, когда жидкий компонент
находится не под давлением Р
своих насыщенных паров, а под любым
другим давлением, фугитивность этого
компонента в жидкой фазе находят по
формуле

(37)

где— фугитивность
жидкости при давлении в системе П
и давлении насыщенных паров Р
соответственно, Па; V_ж
— мольный объем компонента, л/моль,
м3/кмоль;П
— давление в системе, Па; Р
— давление насыщенных паров чистого
компонента, Па; R
— универсальная газовая постоянная,
КДж/(кмольК);Т
— температура системы, К.

Пример 15.Определить
фугитивность паров узкой бензиновой
фракции (М = 100), находящейся при 400°С
и 4,55 МПа. Критические параметры фракцииt_кр= 321°С иР_кр= 3,72 МПа.

Теоретические модели

Вириальное уравнение особенно полезно для описания причин неидеальности на молекулярном уровне (очень немногие газы являются одноатомными), поскольку оно выводится непосредственно из статистической механики:

Zзнак равно1+BVм+CVм2+DVм3+…{\ displaystyle Z = 1 + {\ frac {B} {V _ {\ mathrm {m}}}} + {\ frac {C} {V _ {\ mathrm {m}} ^ {2}}} + {\ frac {D} {V _ {\ mathrm {m}} ^ {3}}} + \ точки}

Где коэффициенты в числителе известны как вириальные коэффициенты и являются функциями температуры.

Вириальные коэффициенты учитывают взаимодействия между последовательно увеличивающимися группами молекул. Например, учитывает взаимодействия между парами, взаимодействия между тремя молекулами газа и т. Д. Поскольку взаимодействия между большим числом молекул редки, вириальное уравнение обычно сокращается после третьего члена.
B{\ displaystyle B}C{\ displaystyle C}

Когда предполагается такое усечение, коэффициент сжимаемости связан с потенциалом межмолекулярных сил φ следующим образом:

Zзнак равно1+2πNАVм∫∞(1-exp⁡(φkТ))р2dр{\ displaystyle Z = 1 + 2 \ pi {\ frac {N _ {\ text {A}}} {V _ {\ text {m}}}} \ int _ {0} ^ {\ infty} \ left (1- \ exp \ left ({\ frac {\ varphi} {kT}} \ right) \ right) r ^ {2} dr}

В статье о реальном газе представлены более теоретические методы расчета коэффициентов сжимаемости.