Приложение а. погрешности вычислений

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁
A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Что такое класс точности манометра, и как его определить

Класс точности манометра является одной из основных величин, характеризующих прибор. Это процентное выражение максимально допустимая погрешность измерителя, приведенная к его диапазону измерений.

Абсолютная погрешность представляет собой величину, которая характеризует отклонение показаний измерительного прибора от действительного значения давления. Также выделяют основную допустимую погрешность, которая представляет собой процентное выражение абсолютного допустимого значения отклонения от номинального значения. Именно с этой величиной связан класс точности.

Существует два типа измерителей давления — рабочие и образцовые.

Рабочие применяются для практического измерения давления в трубопроводах и оборудовании. Образцовые — специальные измерители, которые служат для поверки показаний рабочих приборов и позволяют оценить степень их отклонения. Соответственно, образцовые манометры имеют минимальный класс точности.

Классы точности современных манометров регламентируются в соответствии с ГОСТ 2405-88 Они могут принимать следующие значения:

Таким образом, этот показатель имеет прямую зависимость с погрешностью. Чем он ниже, тем ниже максимальное отклонение, которое может давать измеритель давления, и наоборот. Соответственно, от этого параметра зависит, насколько точными являются показания измерителя. Высокое значение указывает на меньшую точность измерений, а низкое соответствует повышенной точности. Чем ниже значение класса точности, тем более высокой является цена устройства.

Узнать этот параметр достаточно просто. Он указан на шкале в виде числового значения, перед которым размещаются литеры KL или CL. Значение указывается ниже последнего деления шкалы.

Указанная на приборе величина является номинальной. Чтобы определить фактический класс точности, нужно выполнить поверку и рассчитать его. Для этого проводят несколько измерений давления образцовым и рабочим манометром. После этого необходимо сравнить показания обоих измерителей, выявить максимальное фактическое отклонение. Затем остается только посчитать процент отклонения от диапазона измерений прибора.

ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:

Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из

можно записать:

т. е. вес арифметического среднего в n раз больше веса единичного измерения.

Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Максимальная абсолютная погрешность

Процесс зфавновсшивагия в цифровых приборах развертывающего уравновеши.

В цифровых циклических приборах выходной код N приближается к искомому отсчету Nх с одной стороны, сверху или снизу, поэтому при АХп ч 0 максимальная абсолютная погрешность от квантования равна ступени & хк.
 

Здесь: Арн — максимальная абсолютная погрешность величины рн, равная половине единицы разряда последней значащей цифры в табличном значении рн; Ар и АГ — максимальные абсолютные погрешности измерения р и Т соответственно.
 

Абсолютная погрешность температурного предела смеси при использовании в расчете надежных экспериментальных данных по давлению пара чистых компонентов, растворимости и коэффициентам активности, как правило, не превышает максимальной абсолютной погрешности температурного предела компонентов смеси.
 

Абсолютная погрешность при изображении в ячейке чисел с запятой, фиксированной после определенного разряда, не превосходит по величине единицы младшего разряда, то есть, как говорят, максимальная абсолютная погрешность при этом постоянна. https://spb-evacuator.ru.
 

Для учета в модели однократной экстракции NRTL влияния воды, были дополнительно подобраны эмпирические коэффициенты бинарного взаимодействия воды с компонентами системы, применение которых при численных исследованиях существенно уменьшило погрешности моделирования в области содержания воды в экстрагенте выше 8 % об. По выходу рафината и содержанию в нем аренов максимальные абсолютные погрешности в этой области составляют 0 6 и 0 9 %, соответственно. Погрешности расчета по выходу экстракта и содержания в нем аренов снизились до 0 6 и 1 1 %, что составляет 4 8 и 1 4 % относительной по.
 

Следует отметить, что для измерения среднего фазового сдвига рассмотренным методом характерно уменьшение погрешности дискретности по сравнению с имеющей место при измерении одиночного интервала времени. Хотя максимальная абсолютная погрешность дискретности определения длительности одного интервала АГ составляет ГСЧ, результирующая погрешность за время измерения Ткзм уменьшается, так как результаты измерения всех k интервалов АГ суммируются, а возникновение частотной погрешности дискретности положительного или отрицательного знака равновероятно.
 

Рассмотрим погрешность от квантования. Следовательно, максимальная абсолютная погрешность от квантования будет равна единице.
 

Второй способ сводится к увеличению числа импульсов, заполняющих временные ворота, достигаемому умножением частоты исследуемого сигнала. При этом максимальная абсолютная погрешность меняется ( если неизменна длительность ворот), но уменьшается относительная погрешность. Осуществление данного способа сопряжено с применением дополнительного блока — умножителя частоты, что усложняет и удорожает аппаратуру.
 

Максимальную погрешность Дгд Т0 удобно учитывать через эквивалентное случайное изменение числа счетных импульсов Nx на 1 импульс. При этом максимальная абсолютная погрешность дискретизации может быть определена разностью значений частоты / получаемых по формулам (7.4) или (7.5) при Л 1 и Nx, и равна А.
 

Максимальные абсолютные погрешности показаний манометров Мп и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2н — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В противном случае максимальная абсолютная погрешность равна вариации показа ний прибора, которая определяется при тарировании.
 

Максимальные абсолютные погрешности показаний манометров М и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2 — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В ином случае максимальная абсолютная погрешность будет равна вариации показаний прибора, которая определяется при тарировании.
 

Вид кривой У 10 — 4Х2 и ее аппроксимация линейными отрезками.

Точность результата зависит от того, в каком состоянии находится счетчик-интегратор в момент остановки цикла вычисления. Для этого значения получаем максимальную абсолютную погрешность — 5 импульсов младшего разряда.
 

Например, при отсчете или установке визира на логарифмической линейке длиной 250 мм ошибка не превышает 0 1 мм. Таким образом, обычно бывает известна максимальная абсолютная погрешность, получаемая при измерении величины х; обозначим эту погрешность через их.
 

Нормирование

Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й

Нормирование осуществляется по:

• абсолютной;
• относительной;
• приведенной.

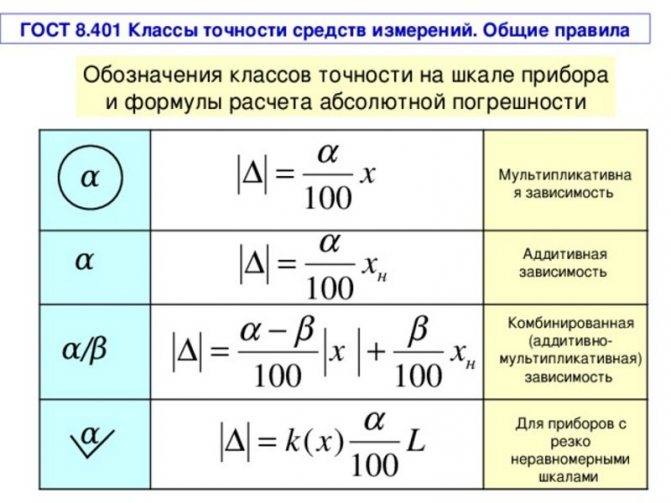
Формулы расчета абсолютной погрешности по ГОСТ 8.401

Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.

Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.

Пределы

Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

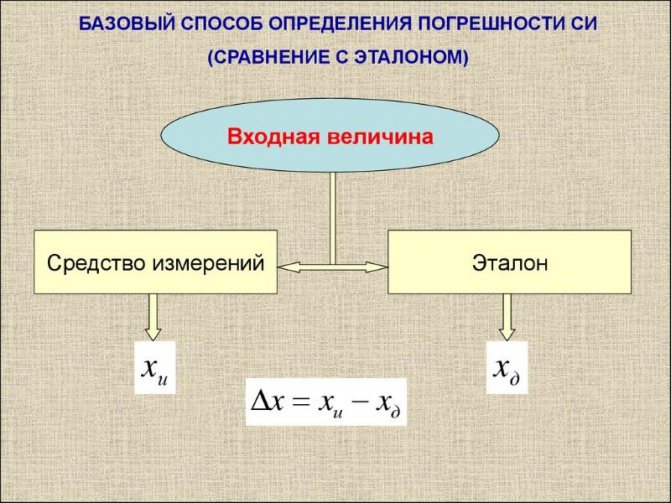
Базовый способ определения погрешности

При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.

Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.

Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5

Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.

Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.

Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.

Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

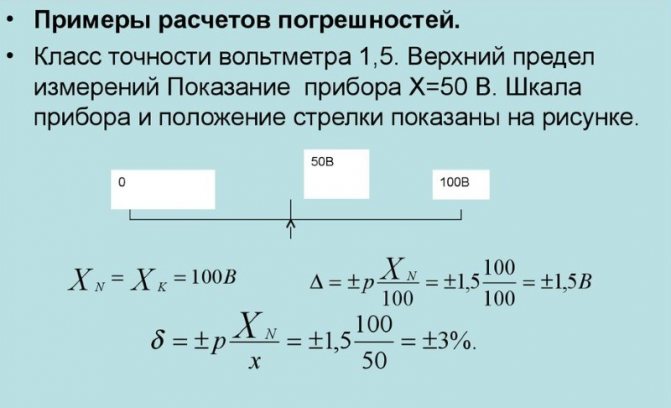
Пример расчета погрешности

Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.

Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.

Виды маркирования

Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.

Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.

Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.

Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.

Электростатические КИП

Эти приборы работают на принципе взаимодействия заряженных электродов, которые разделены диэлектриком. Конструктивно они выглядят практически как плоский конденсатор. При этом, при перемещении подвижной части емкость системы также изменяется.

Наиболее известные из них – это устройства с линейным и поверхностным механизмом. У них немного разный принцип действия. У приборов с поверхностным механизмом емкость изменяется за счет колебаний активной площади электродов

В другом случае важно расстояние между ними

К достоинствам таких устройств относятся небольшая мощность потребления, класс точности ГОСТ, достаточно широкий частотный диапазон и т.д.

Недостатками являются небольшая чувствительность прибора, необходимость экранирования и пробой между электродами.

Определения

Есть верхний и нижний предел погрешности. Обычно оба имеют одинаковый размер и в таком случае называются пределами симметричной погрешности . Пределы погрешности — это всегда суммы, поэтому они указываются без знака.г{\ displaystyle G}

Это относится к (абсолютному) отклонению или (абсолютной) ошибке. Ф.{\ displaystyle F}

|Ф.|≤г{\ displaystyle | F | \ leq G} .

Соответственно, существует относительный предел ошибки таким образом, что относительное отклонение или относительная погрешность применяется
г{\ displaystyle g}ж{\ displaystyle f}

|ж|≤г{\ displaystyle | f | \ leq g} .

Контрольное значение для относительной погрешности подобно правильного значения  ;
Икср{\ displaystyle x_ {r}}

гзнак равног|Икср|{\ displaystyle g = G / | x_ {r} |} .

Основная приведенная погрешность

Определение основной приведенной погрешности измерительного прибора производится путем сравнения показаний испытуемого прибора с эталонным при нормальных условиях работы. В настоящее время отсутствует эталонный расходомер для малых расходов, с которым можно было бы сравнивать показания датчика ДР-2Б. Также не установлены официально нормальные условия работы турбинного датчика подобного типа.
 

Предел допускаемой основной приведенной погрешности по обеспечению уровня сигнала задания не превышает 0 5 % от максимального значения выходного сигнала.
 

Предел допускаемой основной приведенной погрешности ( в % от диапазона измерения) определяет класс точности прибора. Допускается нормировать этот предел раздельно для двух участков диапазона измерения. В таком случае класс точности прибора устанавливают по тому участку диапазона, который имеет более высокий класс точности.
 

Предел допускаемой основной приведенной погрешности фазометров выражается в процентах от нормирующего значения.
 

За величину фактической основной приведенной погрешности принимается наибольшее значение из трех экспериментов.
 

Характеристики ПГС, используемых при поверке преобразователя ДИСК 201.| Пневматическая схема преобразователя ДИСК-201 для определения основной погрешности.

Для определения основной приведенной погрешности преобразователя предварительно корректируют начальные выходные сигналы на первом и на втором диапазонах измерения.
 

Предел допускаемой основной приведенной погрешности показаний не превышает — 0 5 % и записи — 1 0 % от нормирующего значения измеряемой величины. Вариация показаний приборов не превышает половины значения предела допускаемой основной погрешности.
 

Предел допускаемой основной приведенной погрешности воспроизведения программы по выходному сигналу задающего устройства не превышает 1 % от диапазона измерения программы.
 

Для определения основной приведенной погрешности приемника ПЧТ снимают его выходную характеристику. На вход приемника ( лепестки / и 2 модуля У2) от внешнего генератора подают сигнал с частотой, соответствующей нижнему пределу телеизмерения, и напряжением 0 6 В. Изменяя частоту генератора, устанавливают стрелку потенциометра КСП-3, подключенного к выходу ПЧТ, на оцифрованные деления шкалы.
 

Предел допускаемой основной приведенной погрешности показаний прибора и записи на всех отметках шкалы при температуре окружающего воздуха 293 К не превышает соответственно 0 5 и 1 0 % от нормируемого значения. Электрическое сопротивление изоляции цепей прибора должно быть не менее 40 МОм, время оборота диаграммы 24 ч 7 мин, питание прибора 220 В, 50 Гц. Необходимо знать, что не допускается прокладка проводов силовой линии и измерительной цепи в одном жгуте или трубе.
 

Цифры указывают основную приведенную погрешность у в процентах.
 

В каждом случае основная приведенная погрешность показаний и записи вторичного прибора определяется в комплекте с первичным прибором и указывается в выпускном аттестате па комплект.
 

В каждом случае основная приведенная погрешность показаний и записи вторичного прибора определяется в комплекте с первичным прибором и указывается в выпускном аттестате на комплект.
 

Погрешность приборов определяется по основной приведенной погрешности записи в процентах ширины поля записи. В выпускаемых промышленностью приборах ширина поля записи равна 40 или 80 мм. Приборы выпускаются как одноканальными, так и многоканальными. Так, БСП типа Н338 могут иметь 1, 2, 4, 6 и 8 каналов. В многоканальных приборах регистрация производится на одном носителе, но с различными диаграммными лентами типа J1R для каждого канала.
 

Определение погрешности

Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления. Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа.

Необходимо отметить, что таким способом можно посчитать только основную погрешность.

Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.

Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений.

Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.