По какой формуле рассчитывается средняя скорость?

Скорость автомобиля

Скорость доставки груза во многом определяется скоростью движения автомобиля. Различают среднетехническую скорость и эксплуатационную.

Среднетехническая скорость учитывает кратковременные остановки в пути, связанные с регулированием движения и определяется:

Где Тдв — время движения;

L — пробег автомобиля.

На величину среднетехнической скорости влияют:

— состояние дорожного покрытия;

— интенсивность движения;

— динамические свойства автомобиля и его техническое состояние;

— особенности перевозимого груза;

— условия движения (время суток, погодные условия, время года, частота остановок в пути);

— квалификация и психофизиологические качества водителя.

Нормативы среднетехнических скоростей: в городе в зависимости от грузоподъемности автомобиля до 7 тонн — 23 км/час; 7тонн и выше – 22км/час.

При работе за городом: от типа дорожного покрытия

Нормативы среднетехнических скоростей: в городе в зависимости от грузоподъемности автомобиля до 7 тонн — 23 км/час; 7тонн и выше – 22км/час.

При работе за городом: от типа дорожного покрытия.

Таблица «Технические скорости движения грузовых автомобилей при работе за городом»

Группа дорог Тип покрытия Техническая скорость, км/ч

I усовершенствованный (асфальт) 42

II переходный (гравийно-щебеноч.) 33

III низший (грунтовое) 25

При работе во время бездорожья, в карьерах, при движении по целине нормативная техническая скорость снижается до 40%, при перевозке грузов, требующих особой осторожности — до 15%. Нормативные технические скорости не учитывают в груженом или порожнем состоянии движется автомобиль. Скорость порожнего в среднем на 7-15% выше, чем груженого

Результаты натурных наблюдений показывают, что техническая скорость в городских условиях мало зависит от грузоподъемности, а определяется интенсивностью транспортного потока от 29 до 39 км/час; за городом на грунтовых дорогах (2 тип) техническая скорость может составлять до 40 км/час, на междугородных магистралях (1 тип) скорость до 60 км/час

Скорость порожнего в среднем на 7-15% выше, чем груженого. Результаты натурных наблюдений показывают, что техническая скорость в городских условиях мало зависит от грузоподъемности, а определяется интенсивностью транспортного потока от 29 до 39 км/час; за городом на грунтовых дорогах (2 тип) техническая скорость может составлять до 40 км/час, на междугородных магистралях (1 тип) скорость до 60 км/час

Нормативные технические скорости не учитывают в груженом или порожнем состоянии движется автомобиль. Скорость порожнего в среднем на 7-15% выше, чем груженого. Результаты натурных наблюдений показывают, что техническая скорость в городских условиях мало зависит от грузоподъемности, а определяется интенсивностью транспортного потока от 29 до 39 км/час; за городом на грунтовых дорогах (2 тип) техническая скорость может составлять до 40 км/час, на междугородных магистралях (1 тип) скорость до 60 км/час.

Эксплуатационная скорость рассчитывается с учетом кратковременных остановок в пути, связанных с регулированием движения, и простоев автомобилей в пунктах погрузки и разгрузки:

Где Vэксп — эксплуатационная скорость, км/ч;

Lнар — общий пробег автомобиля за время в наряде, км;

Тдв — суммарное время движения за время работы на линии, час ;

Тп-р — суммарный простой в пунктах погрузки разгрузки за время в наряде, час.

Коммерческая скорость (скорость доставки груза) — учитывает все имеющиеся затраты времени, включая время пролеживания груза на промежуточных складах .

Расстояние между ГО и ГП

V ком = ————————————————————— ;

t с момента окончания погрузки до начала выгрузки

Как решать задачи на среднюю скорость

В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:

1. Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
2. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
3. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!

Средняя скорость объекта

Для начала вспомним формулу, по которой решаются все задачи на движение: ​\( S=vt \)​ — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:

Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком.

Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной.

Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть ​\( t=t_1+t_2+\ldots+t_n \)​, причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: ​\( t_n=\dfrac{S_n}{v_n} \)​

Решение задач

А теперь, обогатившись некоторой теорией решим первую из предложенных задач:

Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.

Решение:

1. По условию задачи мы видим, что автомобиль прошёл сначала одну треть, затем вторую треть и последнюю треть. Значит весь его маршрут состоит из трёх участков. Поэтому удобно обозначить длину всего его пути за ​\( 3S \)​
2. Теперь нам необходимо выяснить за какое время автомобиль прошёл каждый из этих промежутков (воспользовавшись формулой ​\( t_n=S_n/v_n \)​). Причем длина каждого из трёх промежутков будет равна S.
   1. Время, за который был пройдена первая треть: ​\( t_1=\dfrac{S}{12} \)​.
   2. Аналогично, найдем время, за которое были пройдены вторая и третья трети всего пути: ​\( t_2=\dfrac{S}{16} \)​ и  ​\( t_3=\dfrac{S}{24} \)​
3. Итак, мы выяснили сколько времени тратит автомобиль на прохождение каждого из отрезков своего пути, значит можем найти сколько он потратил времени всего: ​\( t=t_1+t_2+t_3 \)​. Таким образом: ​\( t=\dfrac{9S}{48} \)​

Теперь мы знаем длину всего пути (\( 3S \)​) и сколько времени автомобиль затратил на прохождение всего пути (\( t=\dfrac{9S}{48} \)​, значит найти среднюю скорость не составит и труда:

Ответ: 16

Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок

-урок: «Как решать задачу на нахождение средней скорости»:

В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.

• #6. Длина хорды
• Как готовиться к ЕГЭ по математике самостоятельно (часть 1)

Постоянная скорость

Описание формулы.

Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.

А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).

Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).

График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.

Это интересно: Как найти по номеру машины владельца — пробиваем авто по базам

Средняя скорость бега человека

Скорость бега зависит как от физической подготовки человека, так и от его природных данных. Первое, что влияет на скорость, – пол и возраст.

• 9-11 км/ч – средняя скорость бега ребёнка до 18 лет
• 9-12 км/ч – средняя скорость бега женщины
• 12-15 км/ч – средняя скорость бега мужчины

До пубертатного периода скорость бега мальчиков и девочек примерно одинаковая. Разрыв в цифрах начинается с момента полового созревания и обусловлен различным гормональным фоном мужчин и женщин. Поэтому к взрослому возрасту, который с точки зрения спортивных нормативов начинается с 18 лет, наблюдается ряд физиологических особенностей, объясняющих, почему женщины медленнее мужчин:

1. У женщин более слабые суставы, а значит, слабее связки и сухожилия.
2. Массовая доля жира в организме мужчины на 10-15% ниже, чем у женщины.
3. Почти на 30% у женщин предельная сила мышц конечностей ниже, чем у мужчин.
4. Объём сердца женщины меньше мужского на 10-20%.
5. Женщины дольше восстанавливаются и более подвержены стрессовым реакциям.
6. У женщин ниже гемоглобин, а значит организм хуже транспортирует кислород.
7. У мужчин уровень тестостерона в 10 раз выше женского, то есть лучше работает опорно-двигательный аппарат.
8. Каденс (шаг) женщины короче мужского.

Хотя стоит отметить, что женщины проще справляются с перепадом температур, у них лучше координация и вестибулярный аппарат. 

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Определение 3

Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к :

υ=lim∆t∆r∆t=drdt=r˙.

Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.

Рисунок 2. Вектор мгновенной скорости υ

Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:

υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

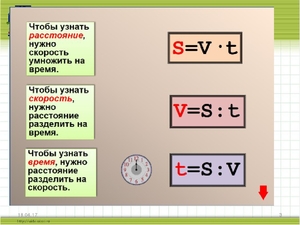
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Аналог «средней температуры» в механике

В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью…», или «первую треть пути пешеход прошагал соскоростью…», и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S 1 = S 2 = … = S n
и точные значения скоростей v 1, v 2, … v
n
, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v
складываются и делятся на n
. В итоге ответ получается неверный.

Средняя скорость

Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.

Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла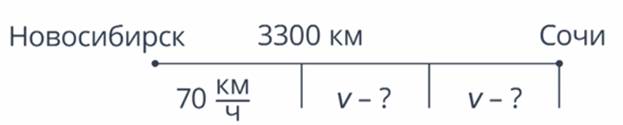

Рис. 6. Иллюстрация к примеру

Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.

Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).

Рис. 7. Средняя скорость

Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.

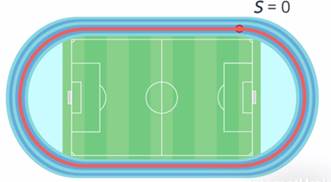
Рис. 8. Перемещение равно 0

На практике чаще всего используется понятие средней путевой скорости.

Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).

Рис. 9. Средняя путевая скорость

Существует еще одно определение средней скорости.

Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.

Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:

Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.

Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).

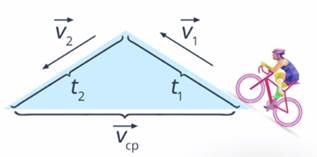
Рис. 10. Иллюстрация к задаче

Дано:Найти:

Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем

Средняя скорость равна:

Полный путь (

Путь подъема на склон равен:

Путь спуска со склона равен:

Время, за которое пройден полный путь, равно:

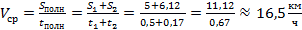
Ответ:

Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.

Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна Мгновенная скорость

Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).

Рис. 11. Спидометр автомобиля показывает мгновенную скорость

Существует еще одно определение мгновенной скорости.

Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).

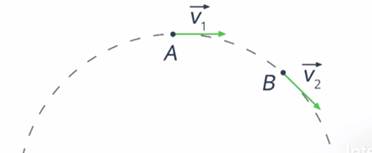
Рис. 12. Мгновенная скорость

Для того чтобы лучше понять данное определение, рассмотрим пример.

Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.

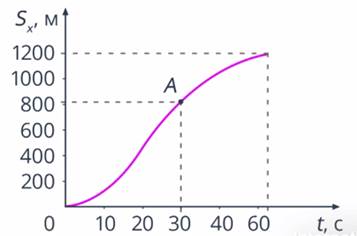
Рис. 13. График зависимости проекции перемещения от времени

На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 14. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 15. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть

A

Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.

Направление мгновенной скорости совпадает с направлением перемещения тела.

Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).

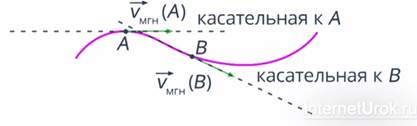
Рис. 16. Направление мгновенной скорости

Скорость в свободных условиях движения

В свободных условиях, когда дорога относительно пустая и вы можете выбирать скорость по своему усмотрению, казалось бы, все просто. Если следовать ПДД, то это 60 км/ч в городе, 80 км/ч на некоторых городских магистралях, 100 км/ч на МКАД, 90 км/ч за городом и 110 км/ч на магистрали. Ну и для любителей поиграть в кошки-мышки с законом, можно на эти значения набросить те самые «беспошлинные» 20 км/ч – ниже этого превышения штрафов нет. Но я сейчас не о штрафах, а о безопасности. Представим, что ограничений скорости нет, как, скажем на автобанах Германии. Значит, можно безнаказанно ехать с любой скоростью. А с какой скоростью ехать безопасно?

Безопасность = наличие резерва

Вспомним, что одно из условий совершения маневра – наличие запаса тяги. И что тяга двигателя – крутящий момент – зависит от показаний тахометра (см. статью «Безопасность вождения и крутящий момент двигателя»). Но способность двигателя разгонять машину зависит также и от скорости: чем ближе скорость движения автомобиля к максимальной, тем сложнее ускориться. Автомобиль хорошо ускоряется при небольших скоростях, и по мере приближения к максимальной скорости разгон происходит все медленнее. Кстати, еще несколько лет назад в технических характеристиках автомобилей BMW на сайте производителя приводилось два показателя времени разгона: для разгона от 0 до 100 км/ч и от 80 до 120 км/ч. Эти показатели были примерно равны между собой. То есть при разгоне с места автомобилю нужно столько же времени для ускорения на 100 км/ч, сколько при разгоне на большой скорости для ускорения всего на 40 км/ч. Чувствуете, к чему я клоню?

Даже если бы и была возможность хоть каждый день ездить на «максималке», все равно этого делать не стоит, потому что любое устройство, в том числе и двигатель, работая на максимуме, не имеет резерва.

Крейсерская скорость

Для сохранения запаса тяги двигателя необходимо ограничивать скорость движения и не приближаться к максимальному значению скорости. А насколько можно приближаться? Где граница? Оптимальная скорость составляет 60-70% от максимальной и называется крейсерской скоростью. Крейсерская скорость движения автомобиля – и есть та разумная граница, которую не стоит превышать, даже на свободных магистралях. То есть крейсерская скорость – максимальная безопасная скорость движения АВТОМОБИЛЯ.

Крейсерская скорость также является самой выгодной скоростью движения в плане соотношения времени в пути к расходу топлива, поэтому воздушные суда летают с крейсерской скоростью.

Перейду к конкретике. Например, для ВАЗ-2110 максимальная скорость по паспорту – 180 км/ч, а крейсерская скорость составляет 108 км/ч (60%). А если взять VW Touareg мощностью 240 л.с., то у него «максималка» по паспорту – 218 км/ч. И для него крейсерская скорость составит 130 км/ч. Не сильно больше, чем у «Лады», правда?

Таким образом, чтобы всегда иметь запас тяги мотора на случай экстренных действий и быть в безопасности, не превышайте крейсерскую скорость своей машины даже в свободных условиях движения. А поскольку максимальная разрешенная скорость в России – 130 км/ч, то нет и проблемы превышения крейсерской скорости Так что соблюдайте правила, и все у вас будет в порядке!

Скорость

Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая –медленее; один человек идет быстрым шагом, другой – не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то определенное время. Допустим, что скорость человека 5 км/ч. То есть за 1 час он прошел 5 километров.

Как находить скорость, время, расстояние? Начнем со скорости. Посмотрите внимательно, в чем она измеряется? Естественно, км/ч, м/с. Существуют и другие единицы измерения, например, км/с (в космонавтике), мм/ч (в биохимии)

Обратите внимание на то, что стоит перед знаком «/» и после. Во-первых, он означает «дробь», а значит, в числителе – мм, км, м, в знаменателе – ч, с, мин

Во-вторых, кажется это напоминает формулу, не правда ли? Километры, метры – расстояние, длина, а час, секунда, минута – время. Вот вам и подсказка. Чтобы проще было запомнить, как находить скорость, посмотрите не единицы измерения (км/ч, м/с). Одними словами:

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

где V0 – начальная скорость движения, a – ускорение, t – время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

V ср = (V0 + V) / 2.

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

а = (V — V0)/ t = (0 – 5)/ 5 = — 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Движение по реке. Скорость течения реки

      В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.

      По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела (скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела  и скорости течения реки.

      Задача 4. Моторная лодка прошла по течению реки   14   км, а затем   9   км против течения, затратив на весь путь   5   часов. Скорость лодки в стоячей воде   5   км/час. Найдите скорость течения реки.

      Решение. Обозначим буквой   v   скорость течения реки и будем считать, что скорость   v   измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.

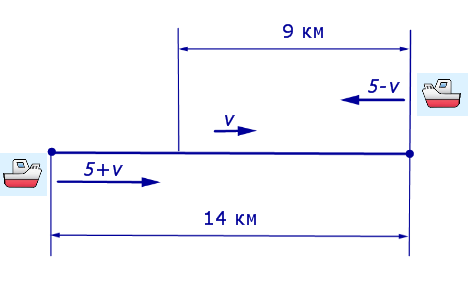
Рис. 3

      Тогда

      5 + v   – скорость, с которой лодка шла по течению реки (в км/час);

      – время движения лодки по течению реки (в часах);

      5 – v   – скорость, с которой лодка шла против течения реки (в км/час);

      – время движения лодки против течения реки (в часах);

      Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути   5   часов:

      Решим это уравнение:

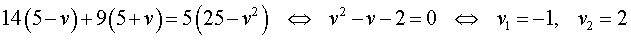
      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   2   км/час.

      Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки   34   км и   39   км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти   75   километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.

      Решение. Обозначим   v_с   (км/ч) скорость лодки в стоячей воде и обозначим   v_р   (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.

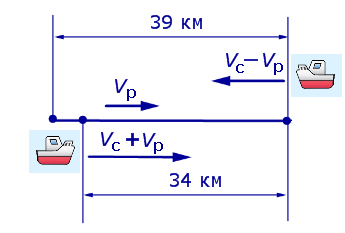
Рис. 4

Рис. 5

      Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:

(3)

      Если ввести обозначение

то, воспользовавшись формулой

v_с = xv_р ,

перепишем уравнение (3) в виде

(4)

      Умножая уравнение (4) на   v_р ,   получим

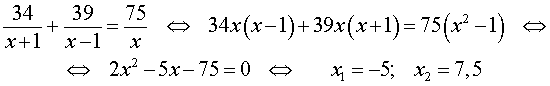
      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   7,5 .

Как найти скорость?

Чтобы найти скорость тела в определенный момент времени, найти начальную скорость или конечную, необходимо для начала разобраться с типом движения. Если оно равномерное, то все достаточно просто. Для того чтобы найти скорость в этом случае, следует просто поделить пройденное телом расстояние на прошедшее время. Это и будет ответ. Немного сложнее дело обстоит в том случае, если движение равноускоренное или равнозамедленное.

Допустим, что тело в течение некоторого периода времени ускоряется. Вот одна из формул, которая может быть применена к задаче подобного рода: S = V0t +(-) at^2/2. В выражении в качестве результата (левая часть уравнения) указано пройденное телом расстояние. В правой части у нас слева направо располагается начальная скорость, время, ускорение. Почему указаны два знака? Если тело разгоняется, ускорение будет положительным, перед слагаемым будет ставиться знак “плюс”. Если ускорение отрицательное, перед слагаемым будет ставиться знак “минус”.

По теме: методические разработки, презентации и конспекты

Урок разработан в соответствии с ФГОС. По типу уроков является проблемным.

Презентация к уроку 5 4 класс учебник М.З. Биболетова — содержит материал для фонетической и лексической разминки, грамматические задания и правила «Построение специальных вопросов».

Презентация выполнена к уроку окружающего мира в 4 классе, УМК «Гармония» по теме «Время: Как человек научился считать время».

Решение задач на время, повторение видов углов, и таблиц единиц длины, массы, площади.

Проверочная работа по теме «Время» для 2 класса, система развивающего обучения Занкова. В работе два варианта, в каждом шесть заданий. Задание №1 (Реши задачу) обязательно для всех. Из остальных .

Методическая разработка открытого урока «Простое прошедшее время» включает в себя план-конспект к уроку и презентацию по уроку.

Контрольная работа состоит из 6 заданий, которые включают в себя не только повторение грамматики, но и лексики. В работе используется лексика по теме: «Погода». Также есть задание на обобщение.

Оптимальная скорость для автомобиля — второй фактор выбора режима поездки

Главным критерием выбора скоростного режима являются далеко не возможности машины, а ваши соображения о безопасности и уверенности поездки. Если вы считаете, что ехать со скоростью 90 км/ч при данных условиях опасно, то лучше выбрать более комфортный и уверенный режим. Тем не менее, существуют определенные рекомендации от производителей.

Первое, о чем стоит вспомнить в таком контексте разговора, является средний расход. Если вы будете поддерживать скорость машины на уровне 90 километров в час, то расход будет максимально близким к паспортным показателям расхода на трассе. Многие водители переживают по поводу того, что их машина на трассе расходует больше топлива, чем указано в документах. Происходит это по таким причинам:

• на обгоне автомобиль вынужден потреблять в разы больше топлива в силу необходимости быстрого разгона;
• постоянное торможение и трогание с места в пробке или на различных преградах также дает плюс к расходу;
• движение на скорости свыше 100 километров в час начинает значительно увеличивать расход бензина;
• производитель рассчитывает трассовые режимы поездки на среднюю скорость 90 километров в час;
• под данный показатель происходит настройка всех функций и узлов автомобиля, передаточных числе и двигателя.

Именно по этим причинам средние показатели расхода часто оказываются на порядок больше паспортных замеров. При определении расхода в трассовом режиме для технических характеристик машины производитель выполняет тестирование транспорта не треке, где машина едет с постоянной одной рекомендованной скоростью. Именно это позволяет достичь столь занимательных цифр расхода топлива.

Для получения максимальных выгод в расходе топлива и прочих характеристиках вашего автомобиля экспериментируйте и пробуйте разные режимы поездки. Не лишни будет и почитать отзывы о том, как люди эксплуатируют ваш тип транспорта. Это поможет максимально упростить эксплуатацию машины, сделать меньшим расход топлива и предсказать любые особенности поведения транспортного средства. Помните, что скорость должна быть оправданной. Предлагаем подборку видео ДТП, случившихся в частности из-за высокой скорости: