Формула скорости

Содержание:

Взаимосвязь скорости, времени, расстояния
Взаимосвязь скорости, времени, расстояния
С чем связано расстояние?
Скорость в физике
Примеры из жизни
Как решать задачи на среднюю скорость
В чем измеряются?
Тормозной путь автомобиля при скорости 60 кмч
- - Тормозной путь на сухом асфальте
  - Тормозной путь на покрытии: снег, лед, мокрый асфальт
Где упоминается скорость тела?
ВИДЕО: Задачи на движение
Ход урока
какой буквой в алгебре обозначается время
Примеры решения задач
Средняя скорость

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

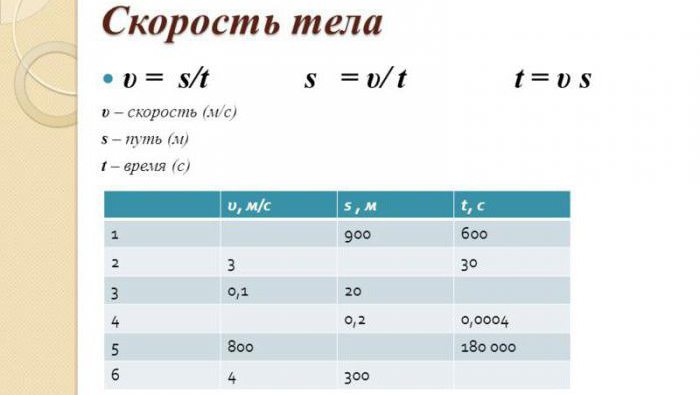
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Взаимосвязь скорости, времени, расстояния

Проблемы с датчиком скорости и распиновка разъема датчика скорости

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

Источник

С чем связано расстояние?

Формула для расчета расхода топлива автомобиля и способы его оптимизации

Понятие «расстояние» не может существовать само по себе, оно должно играть какую-то роль. Например, вы едете на велосипеде в школу, а не идете пешком, потому что опаздываете. Как мы говорили ранее, наш путь до школы прямой. Можно спокойно ехать по тротуару. Естественно, если перемещаться пешком, то получится дольше, чем проделать путь на велосипеде. В чем же здесь дело? Речь, разумеется, идет о скорости, с которой перемещаетесь. Позже мы увидим формулы, которые подскажут, как найти расстояние. Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.

Итак, у нас появились еще два параметра:

t – время,

v – скорость.

Все будет намного интереснее, если научитесь работать с формулами и находить неизвестное с помощью дробей. Напомним лишь только правило из математики: все, что находится рядом с неизвестным, идет в знаменатель (то есть вниз дроби). Например, формула расстояния (физика) – это произведение времени и скорости. А в других случаях – дроби. Посмотрите на картинку, в которой изображено, как находить расстояние, скорость и время. Обязательно потренируйтесь и разберитесь, как получаются такие формулы. Все следует только из законов математики, ничего выдуманного в этих формулах нет. Давайте-ка потренируемся (не подглядывайте): какой буквой обозначается расстояние в физике?

Скорость в физике

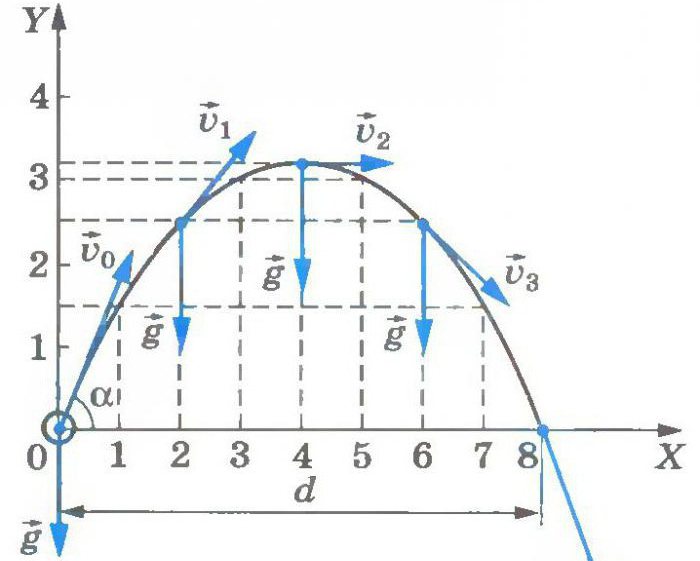
Физика: формула удельного сопротивления и закон ома

Нередко ученики, которые впервые (а возможно и повторно) знакомятся с азами (можно их так назвать) кинематики, задаются вопросом о том, как найти начальную скорость

Это действительно важно, поскольку множество задач из первой части материалов, которые предлагаются ученику для самостоятельного решения на экзамене в 9 и 11 классе, имеют целью нахождение начальной скорости либо величин, каким-либо образом связанных с ней

Да и вообще, хотелось бы отметить, что в определенных случаях знание формул кинематики (в том числе и формулы начальной скорости при соответствующем виде движения) поможет решить даже задачу из последней части. Разумеется, на соответствующую тему. Итак, как найти начальную скорость в задачах по физике? Давайте вспомним, какие формулы даются в разделе кинематики для использования их в целях нахождения неизвестных величин.

Примеры из жизни

Что же такое расстояние? Как обозначается расстояние в физике, мы уже уяснили. Теперь разберемся с понятием.

Представьте себе, что вы сейчас стоите возле своего дома. Ваша задача – дойти до школы. Дорога все время прямая. Идти от силы около двух минут. От дверей подъезда до школьных дверей 200 метров. Это и есть расстояние. Как будет выглядеть описание вашей прогулки от дома до школы?

S=200 м.

Почему мы не написали «метров», а ограничились только буквой? Потому что такое вот сокращенное буквенное обозначение. Чуть позже познакомимся и с другими параметрами, которые связаны с расстоянием.

А теперь представьте, что путь от дома до магазина извилистый. Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.

Как решать задачи на среднюю скорость

В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:

Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!

Средняя скорость объекта

Для начала вспомним формулу, по которой решаются все задачи на движение: $ S=vt $ — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:

Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком.

Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной.

Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть $ t=t_1+t_2+\ldots+t_n $, причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: $ t_n=\dfrac{S_n}{v_n} $

Решение задач

А теперь, обогатившись некоторой теорией решим первую из предложенных задач:

Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.

Решение:

По условию задачи мы видим, что автомобиль прошёл сначала одну треть, затем вторую треть и последнюю треть. Значит весь его маршрут состоит из трёх участков. Поэтому удобно обозначить длину всего его пути за $ 3S $
Теперь нам необходимо выяснить за какое время автомобиль прошёл каждый из этих промежутков (воспользовавшись формулой $ t_n=S_n/v_n $). Причем длина каждого из трёх промежутков будет равна S.
1. Время, за который был пройдена первая треть: $ t_1=\dfrac{S}{12} $.
2. Аналогично, найдем время, за которое были пройдены вторая и третья трети всего пути: $ t_2=\dfrac{S}{16} $ и $ t_3=\dfrac{S}{24} $
Итак, мы выяснили сколько времени тратит автомобиль на прохождение каждого из отрезков своего пути, значит можем найти сколько он потратил времени всего: $ t=t_1+t_2+t_3 $. Таким образом: $ t=\dfrac{9S}{48} $

Теперь мы знаем длину всего пути ($ 3S $) и сколько времени автомобиль затратил на прохождение всего пути ($ t=\dfrac{9S}{48} $, значит найти среднюю скорость не составит и труда:

Ответ: 16

Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок

-урок: «Как решать задачу на нахождение средней скорости»:

В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.

#6. Длина хорды
Как готовиться к ЕГЭ по математике самостоятельно (часть 1)

В чем измеряются?

Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать

Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема

Дальше будет сложнее. Давайте приступим:

S – расстояние – метр, километр , ;

v – скорость – метров в секунду, километров в час [м/с], [км/ч] (в случае космических скоростей может применяться километр в секунду;

t – время – секунда, минута, час , ,.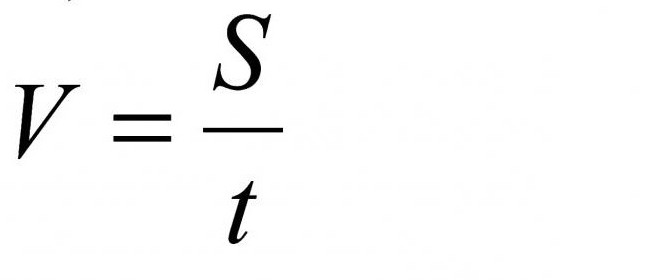

Обратите внимание, как обозначается скорость. Правильно, дробью

А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.

Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.

https://skysmart.ru/articles/mathematic/vremya-skorost-rasstoyanie
http://shpargalkablog.ru/2015/11/point-line-straight-ray-segment.html
https://ktonanovenkogo.ru/voprosy-i-otvety/diametr-chto-ehto-takoe.html
https://autogear.ru/article/238/455/kak-oboznachaetsya-rasstoyanie-v-fizike-interesnyie-primeryi/

Тормозной путь автомобиля при скорости 60 кмч

Деформация кузова при столкновении на скорости 60 км/ч

Длина остановочного пути

также зависит не только от водителя, но и от других сопутствующих факторов: от качества дороги, скорости движения, погодных условий, состояния тормозной системы, устройства тормозной системы, шин автомобиля и многих других.

Обратите внимание, что вес легкового автомобиля не влияет на длину тормозного пути. Это связано с тем, что вес автомобиля увеличивает инертность автомобиля при выполнении торможения, препятствуя при этом торможению, но увеличивает сцепление шин с дорогой благодаря увеличенной массе авто. Эти физические свойства компенсируют друг друга, при этом практически не оказывая влияние на длину тормозного пути

Эти физические свойства компенсируют друг друга, при этом практически не оказывая влияние на длину тормозного пути.

Скорость торможения напрямую зависит от способа торможения. Резкий тормоз

до упора, приведет к заносу или движению машины юзом (если машина не оборудована системой ABS).

Постепенное нажатие

на педаль применяется когда на дороге хорошая видимость и спокойная обстановка, оно не подходит для экстренных ситуаций.При прерывистом нажатии можно потерять управляемость, но зато быстро остановиться. Также возможноступенчатое нажатие (схоже по эффекту с системой АБС).

Существуют специальные формулы, которые позволяют определить длину тормозного пути. Мы попробуем просчитать формулу по разным условиям, в зависимости от типа дорожного покрытия.

Тормозной путь на сухом асфальте

Вспоминаем уроки физики, где ?

– это коэффициент трения,g – ускорение свободного падения, аv – скорость движения машины в метрах в секунду.

Ситуация следующая: едет водитель на автомобиле Lada скорость которого 60 км/час. Буквально в 70 метрах идет женщина преклонного возраста, которая забыв о правилах безопасности спешно догоняет маршрутное такси (стандартная ситуация для России).

Воспользуемся этой самой формулой: 60 км/ч = 16,7 м/сек. У сухого асфальта коэффициент трения равняется 0,7 , g – 9,8 м/с. На самом деле, в зависимости от состава асфальта, он равен от 0.5 до 0.8, но всё же возьмем усредненное значение.

Полученный по формуле результат 20,25 метров. Естественно, что данное значение уместно лишь для идеальных условий, когда на машину установлена качественная резина и тормозные колодки, тормозная система исправна, при торможении вы не уходите в юз и не теряете управление, от множества других идеализированных факторов, которые не встречаются в природе.

Также для перепроверки результата, существует еще одна формула определения тормозного пути

S = Кэ * V * V / (254 * Фс) , где Кэ – тормозной коэффициент, для легковых авто он равняется единице; Фс – коэффициент сцепления с покрытием 0,7 (для асфальта).

Подставляем скорость движения транспортного средства в км/ч.

Получается, что тормозной путь 20 метров для скорости 60 км/ч, (для идеальных условий), в том случае если торможение будет резким и без юза.

Тормозной путь на покрытии: снег, лед, мокрый асфальт

Автомобили BMW на испытаниях Коэффициент сцепления помогает обозначить длину остановочного пути при разных дорожных условиях. Коэффициенты для разных дорожных покрытий

Сухой асфальт – 0,7
Мокрый асфальт – 0,4
Укатанный снег – 0,2

Попробуем подставить эти значения в формулы, и найдем значения длины тормозного пути для дорожного покрытия в разное время года и при разных погодных условиях

Мокрый асфальт – 35,4 метра
Укатанный снег – 70,8 метра
Лед – 141,6 метра

Получается, что на льду длина тормозного пути практически в семь раз

выше, относительно сухого асфальта (так же как и подставляемый коэффициент). На длину тормозного пути влияет качество зимней резины, физические свойства.

Тестирование показало, что с системой АБС остановочный путь существенно снижается, но все же при гололеде и снеге АБС не влияет, а наоборот ухудшает эффективность торможения, если ее сравнивать с тормозной системой без ABS. Тем не менее, в АБС по большей мере все зависит от настроек и наличия системы распределения тормозного усилия (ЕБД).

Преимущество АБС в зимнее время

– полный контроль над управлением автомобиля, что сводит к минимуму возникновения неуправляемого заноса при выполнении торможения. Принцип работы АБС схож с выполнением ступенчатого торможения на автомобилях без АБС.

Система АБС уменьшает тормозной путь на: сухом и мокром асфальте, укатанном гравии, разметке .

На льду и укатанном снеге использование АБС увеличивает тормозной путь на 15 — 30 метров, но позволяет сохранить контроль над машиной, без увода машины в занос. Этот факт следует учитывать.

Где упоминается скорость тела?

На самом деле, в реальном мире мы сталкиваемся со скоростью ежесекундно. Если так подумать, на Земле постоянно что-то да находится в движении. Вы можете попробовать возразить, ограничившись, например, пределами своей комнаты. То есть, по мнению некоторых людей, ночью в комнате ничего не движется. Кровати, шкафы, стулья, стол и прочие предметы находятся на своих местах, в то время как сам человек спит, то есть не движется.

Следовательно, скорость любого элемента данной системы (комнаты, как мы условились считать) равна нулю. Да, в этом что-то есть, и с одной стороны, человек, выдвинувший такое предположение, мог оказаться правым. Но не следует забывать о том, что своеобразную систему представляет собой сама наша планета Земля, а не только предметы, которые на ней находятся. А ведь все мы знаем, что ежесекундно Земля вращается вокруг своей оси. В этой системе отсчета все тела, находящиеся в пределах планеты, также совершают движение. Поэтому говорить о том, что предмет, который, казалось бы, не двигается, находится в абсолютном покое, нельзя. Это первое, что нужно было бы сказать о скорости тела.

С детской скамьи мы учимся решать много задач не только физического, но и математического характера. Их в настоящее время не так много, и ставка делается больше на гуманитарные дисциплины наподобие иностранного языка, хотя они не должны преподаваться в ущерб родному языку и техническим дисциплинам. Но речь немного не об этом. Так вот, понятие скорости тела мы можем встретить не только в задачах по физике, хотя там она встречается, пожалуй, наиболее часто. Несколько реже, но все же фигурирует скорость тела и в задачах по математике.

Наверняка все помнят эти до ужаса ненавистные (в большинстве случаев) задачи, в которых требовалось найти, через сколько времени встретятся два автомобиля, если они движутся с такими-то скоростями. Условия при этом могут быть самые разные. То движение происходит по круговой траектории (спортсмены на велосипедах или мотоциклах), то по прямолинейной траектории. В общем, задач множество. И как бы там ни было, а наша задача заключается в том, чтобы понять, что нужно делать, столкнувшись с вопросом о том, как найти скорость в том или ином случае.

ВИДЕО: Задачи на движение

Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Сравните скорость Зелибобы и Кубика. ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, служащие для записи математических понятий, предложений и выкладок.

Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.

Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета.

Ход урока

Организационный момент

Психологический настрой

Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.

Учитель
: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.

Сообщение темы и цели урока

Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.

(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).

Слайд № 1

Девиз нашего урока: «Один за всех, все за одного»

Работа в парах

На партах карточки с примерами:

Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)

Минутка чистописания

Слайд № 2

2 4 6 8 10 (образец в тетради)

Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?

Устная работа с остальными учениками:

В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?

Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?

Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?

За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?

Слайд № 3

Физминутка

Слайд № 4

Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам — шофер (Имитируют управление автомобильным рулем.)
И сам — мотор. (Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)

Первичное закрепление

Слайд № 5

Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?

Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?

Слайд № 6

Решение задачи № 2

Автобус

S — 90 км 90: 45= 2 часа
T — ?
V — 45 км/ч

Легковая машина

S — 270 км 270: 90 = 3 часа
T — ?
V — 90 км/ч

Давайте подведем итог урока

Чем занимались на уроке?

Что запомнили?

Рефлексия

Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.

Красный — радость
Жёлтый — приятное
Зелёный — спокойное
Синий — грустное
Фиолетовый — тревожный
Оранжевый — удовлетворение
Чёрный — неудовлетворение

И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.

Наш закончен урок —
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!

Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.

какой буквой в алгебре обозначается время

Самая простая формула скорость, это длина деленная на расстояние. Латинской буквой V. Такое обозначение используется и в математике, и в физике. Начатки буквенного обозначения и исчисления возникают в позднеэллинистич.

В различных странах стихийно появляются 3. м. для нек-рых действий и для степеней неизвестной величины. Кто готов назвать их в порядке возрастания? В единицах длины).

Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы. Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. Вы назвали формулу, по которой находят скорость движения. Этой формулой вы будете пользоваться и в старших классах.

Примеры решения задач

Задание. Движение материальной точки А задано уравнением: $x=2 t^-4 t^$ . Точка начала свое движение при t=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

Формула скорости не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Скорость материальной точки является функцией от времени вида:

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$ begin10 t-t^=10(2.2) t_=5+sqrt approx 8,8(c) ; t_=5-sqrt approx 1,13(c) end $$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

При решении уравнения (2.3) нам подойдет корень равный:

Ответ. 1) $x=0 mathrm

m>$ 2) $t_=8,8 mathrm, t_=1,13 c, t_=11 c$

Класс: 4

Цели:

закрепить знания нахождения скорости, времени, расстояния;
ввести формулы;
учиться решать задачи с этими величинами по формулам и без них;
развивать мышление и память;
прививать любовь к математике.

1. Организация учащихся.

2. Сообщение темы.

— Сегодня на уроке мы закрепим знания нахождения скорости, времени, расстояния. Будем учиться решать задачи с помощью формул.

— А работать мы будем в форме соревнований трех команд:

1 ряд — автомобилисты
2 ряд — летчики
3 ряд — мотоциклисты

— Баллы будем выставлять на доске

3. Соотнести записи с картинкой.

— Как вы думаете, что написано на доске? (Скорости)

— Соотнесите их с нужной картинкой.

(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50 км/ч,250 км/ч.

Автобус, самолет, ракета, пешеход, поезд, велосипедист , автомобиль, пароход, мотоциклист) Каждая команда выставляет по 3 ученика.

— Как вы понимаете км/сек, км/ч, м/мин.

а) В тетрадь записываете ответ с наименованием.

Таблица на интерактивной доске.

Средняя скорость

Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.

Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла

Рис. 6. Иллюстрация к примеру

Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.

Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).

Рис. 7. Средняя скорость

Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.

Рис. 8. Перемещение равно 0

На практике чаще всего используется понятие средней путевой скорости.

Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).

Рис. 9. Средняя путевая скорость

Существует еще одно определение средней скорости.

Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.

Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:

Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.

Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).

Рис. 10. Иллюстрация к задаче

Дано:Найти:

Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем

Средняя скорость равна:

Полный путь (

Путь подъема на склон равен:

Путь спуска со склона равен:

Время, за которое пройден полный путь, равно:

Ответ:

Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.

Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна Мгновенная скорость

Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).

Рис. 11. Спидометр автомобиля показывает мгновенную скорость

Существует еще одно определение мгновенной скорости.

Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).

Рис. 12. Мгновенная скорость

Для того чтобы лучше понять данное определение, рассмотрим пример.

Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.

Рис. 13. График зависимости проекции перемещения от времени

На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 14. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 15. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть

Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.

Направление мгновенной скорости совпадает с направлением перемещения тела.

Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).

Рис. 16. Направление мгновенной скорости